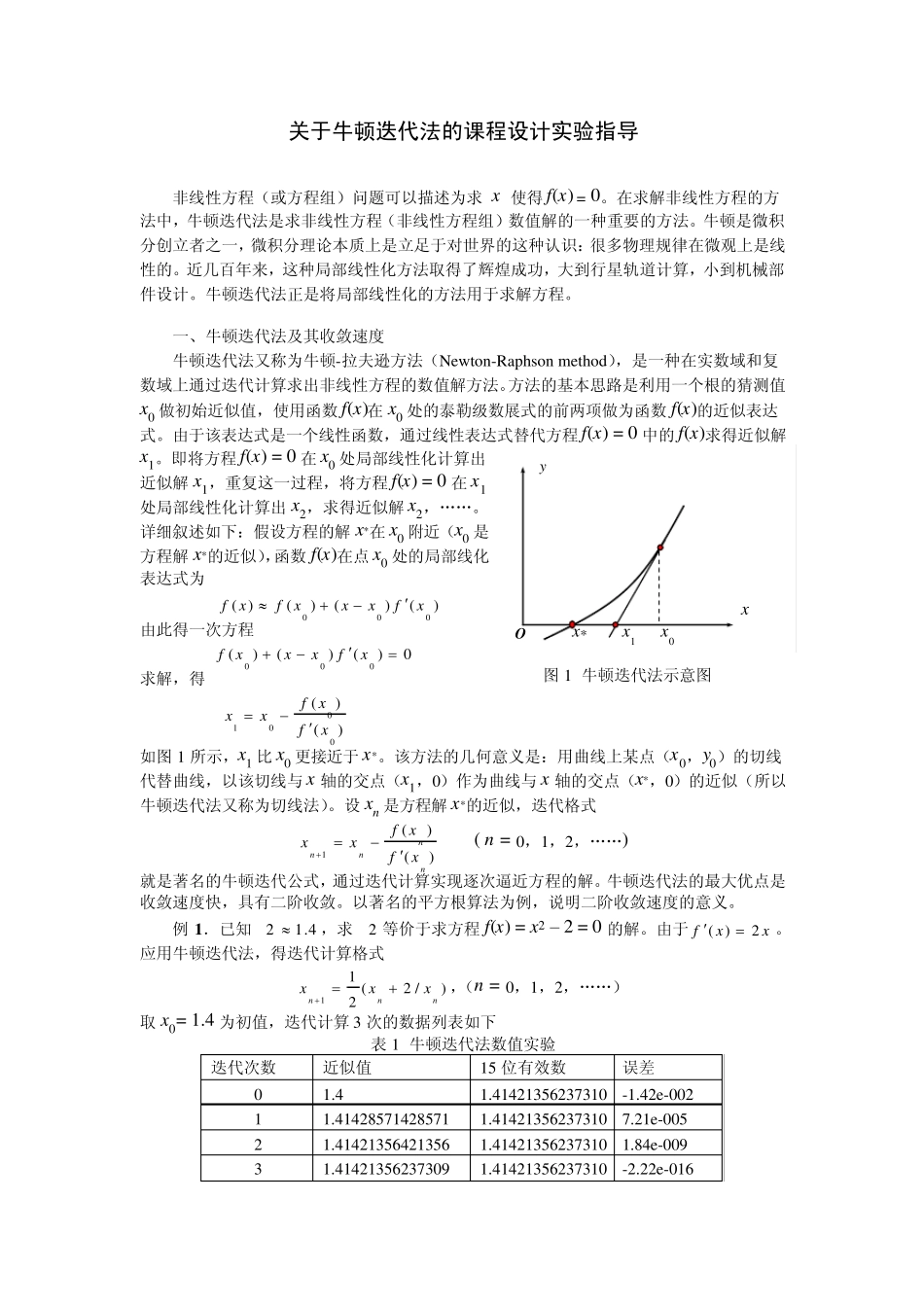
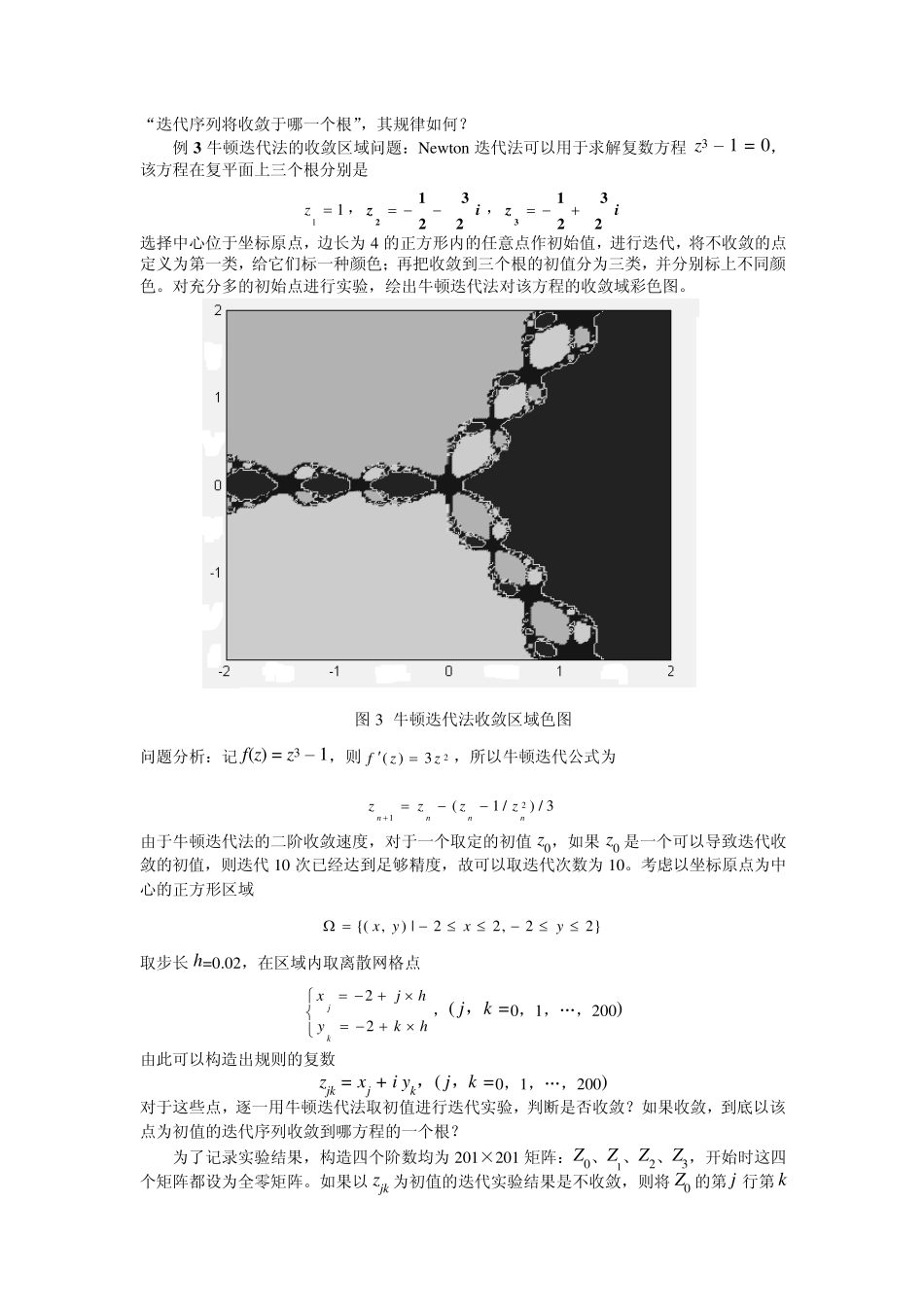
y x O x* x1 x0 关于牛顿迭代法的课程设计实验指导 非线性方程(或方程组)问题可以描述为求 x 使得f(x) = 0。在求解非线性方程的方法中,牛顿迭代法是求非线性方程(非线性方程组)数值解的一种重要的方法。牛顿是微积分创立者之一,微积分理论本质上是立足于对世界的这种认识:很多物理规律在微观上是线性的。近几百年来,这种局部线性化方法取得了辉煌成功,大到行星轨道计算,小到机械部件设计。牛顿迭代法正是将局部线性化的方法用于求解方程。 一、牛顿迭代法及其收敛速度 牛顿迭代法又称为牛顿-拉夫逊方法(New ton-Raphson method),是一种在实数域和复数域上通过迭代计算求出非线性方程的数值解方法。方法的基本思路是利用一个根的猜测值x0 做初始近似值,使用函数f(x)在x0 处的泰勒级数展式的前两项做为函数f(x)的近似表达式。由于该表达式是一个线性函数,通过线性表达式替代方程f(x) = 0 中的f(x)求得近似解x1。即将方程f(x) = 0 在x0 处局部线性化计算出近似解x1,重复这一过程,将方程f(x) = 0 在x1处局部线性化计算出 x2,求得近似解x2,„„。详细叙述如下:假设方程的解x*在x0 附近(x0 是方程解x*的近似),函数f(x)在点 x0 处的局部线化表达式为 )()()()(000xfxxxfxf 由此得一次方程 0)()()(000xfxxxf 求解,得 )()(0001xfxfxx 如图 1 所示,x1 比 x0 更接近于x*。该方法的几何意义是:用曲线上某点(x0,y0)的切线代替曲线,以该切线与 x 轴的交点(x1,0)作为曲线与 x 轴的交点(x*,0)的近似(所以牛顿迭代法又称为切线法)。设xn 是方程解x*的近似,迭代格式 )()(1nnnnxfxfxx ( n = 0,1,2,„„) 就是著名的牛顿迭代公式,通过迭代计算实现逐次逼近方程的解。牛顿迭代法的最大优点是收敛速度快,具有二阶收敛。以著名的平方根算法为例,说明二阶收敛速度的意义。 例 1 .已知4.12 ,求2 等价于求方程f(x) = x2 – 2 = 0 的解。由于xxf2)(。应用牛顿迭代法,得迭代计算格式 )/2(211nnnxxx,(n = 0,1,2,„„) 取x0= 1.4 为初值,迭代计算3 次的数据列表如下 表 1 牛顿迭代法数值实验 迭代次数 近似值 15 位有效数 误差 0 1.4 1.41421356237310 -1.42e-002 1 1.41428571428571 1.41421356237310 7.21e-005 2 1.41421356421356 1.41421356237310 1.84e-009 3 1.4142135...