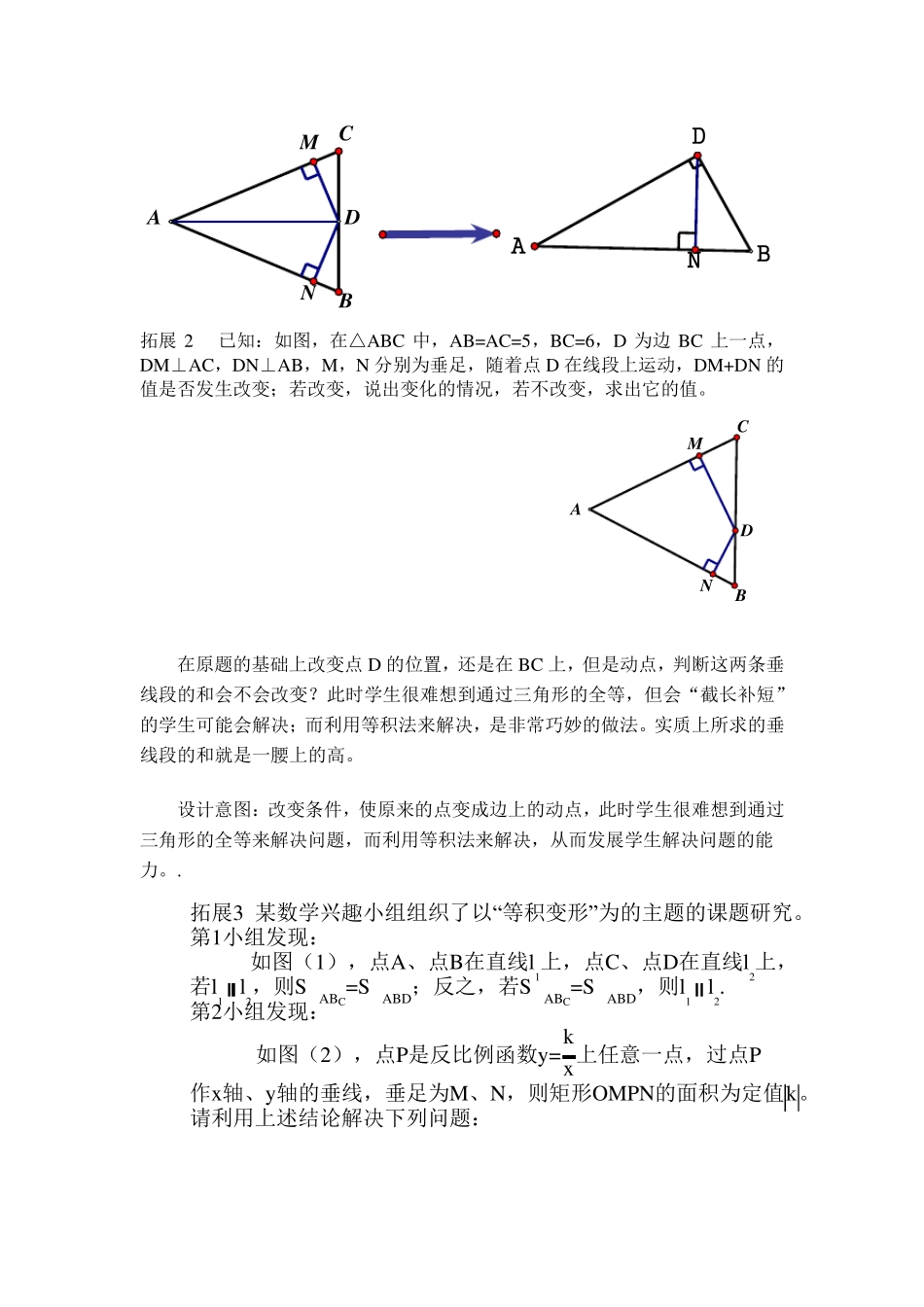
说题稿 实验中学 徐顺从 原题 已知:如图,AD 垂直平分BC,D 为垂足,DM⊥AC,DN⊥AB,M,N 分别为垂足,求证:DM=DN NMDBCA 一、说背景与价值 本题选自八年级上第一章《三角形的初步知识》之《1.5 三角形全等的判定4》的 课内练习2。解决此题涉及的知识有垂直的定义,垂直平分线的定义及性质,三角形全等的判定,角平分线的性质,三角形的面积等。 本习题是在学生学习三角形全等的判定定理“AAS”,及角平分线的性质的基础上给出的。课本设置此练习的目的旨在巩固三角形全等的判定及角平分线的性质。大部分学生想到利用三角形全等,然而解题的方法较多,需要学生发散思维,充分联系已知与求证,综合运用已学的知识来解决,在众多的方法中进行选优,从而获得一定的解题经验。 二、说教学与改进 学生已经学会了三角形全等的判定定理“SSS”,“SAS”,“ASA”,“AAS”,对于证明相等的线段,基本上具备了解决此题的知识储备和技能。而学生往往会思维定势,联想到证明三角形全等,而忽视了此时证明的是垂线段这个重要信息,缺乏相应的想象。 学生可能的做法: 1、先证明△ADC≅ △ADB 得∠B=∠C,再证明△DCM≅ △DBN,得到 DM=DN; 2、先证明△ADC≅ △ADB 得∠CAD=∠BAD,再证明△DAM≅ △DAN,得到 DM=DN; 3、先证明△ADC≅ △ADB 得 AD 是角平分线,再利用角平分线的性质,得到 DM=DN; 4、先由中垂线的性质证明 AB=AC,再由三角形的中线将三角形的面积二等分, 得ADBADCSS,由 DM⊥AC,DN⊥AB,得到 DM=DN。 在原先的教学中,让学生思考后回答,发现大部分学生是第1,2 种解法,很少出现第3,4 的解法,然后再追问,还有其他的方法吗?能利用今天学过的知识 来解决吗?能利用角平分线的性质吗?终于有了第3 种方法,可是学生缺乏想象,这样的教学效果不好。 针对很少学生想出方法3,方法4,以及充分发挥这道题目的价值,我在第二节课时对教学进行了如下的改进。首先是讲解角平分线的性质时做好铺垫,在讲解角平分线时,引导学生理解角平分线上的点到角两边的距离相等,这个距离指的是垂线段的长度。以及应用角平分线性质时具备3 个条件:角平分线,两条垂线段。其次在讲解时让学生说出各自的解法,当大部分学生出现前两种方法时,进行如下的引导启发。引导关注条件,所求证的DM=DN,与它相关的条件是什么?DM⊥AC,DN⊥AB,发现所证明的两条线段与众不同,它们是垂线段,再启发学生对垂线段展开...