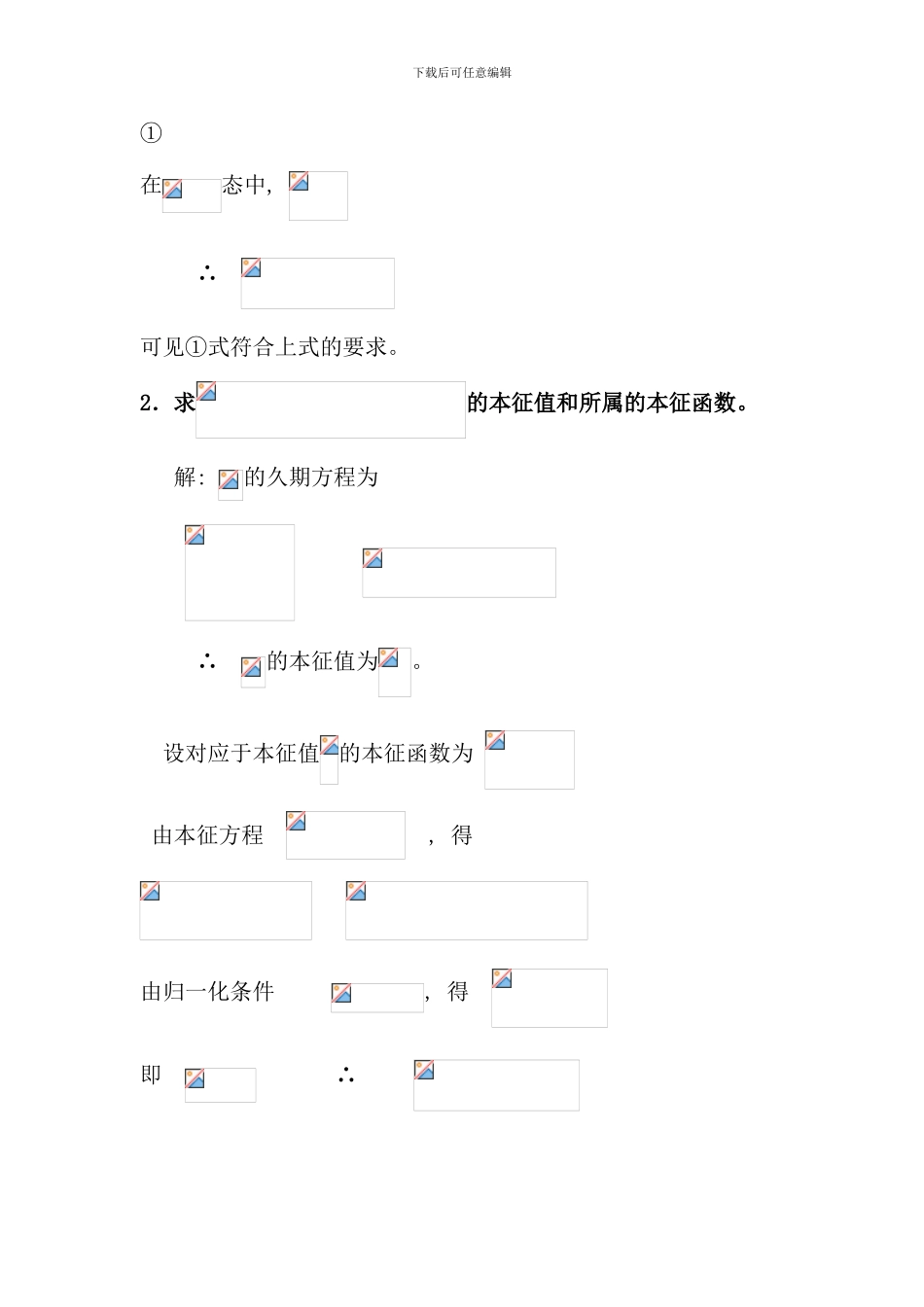
下载后可任意编辑第六章 全同粒子体系习题解1.求在自旋态中, 和的不确定关系: 解: 在表象中、 、 的矩阵表示分别为 ∴ 在态中 讨论: 由、 的对易关系 [, ] 要求 下载后可任意编辑①在态中, ∴ 可见①式符合上式的要求。2.求的本征值和所属的本征函数。 解: 的久期方程为 ∴ 的本征值为。设对应于本征值的本征函数为 由本征方程 , 得 由归一化条件 , 得 即 ∴ 下载后可任意编辑对应于本征值的本征函数为 设对应于本征值的本征函数为 由本征方程 由归一化条件, 得 即 ∴ 对应于本征值的本征函数为 同理可求得的本征值为。其相应的本征函数分别为 3.求自旋角动量方向的投影 本征值和所属的本征函数。 在这些本征态中, 测量有哪些可能值? 这些可能值各以多大的几率出现? 的平均值是多少? 下载后可任意编辑解: 在 表象, 的矩阵元为其相应的久期方程为 即 因此的本征值为。设对应于的本征函数的矩阵表示为, 则由归一化条件, 得下载后可任意编辑 可见, 的可能值为 相应的几率为 下载后可任意编辑同理可求得 对应于的本征函数为在此态中, 的可能值为 相应的几率为 讨论: 算符的本征值为, 而 z 方向为空间的任意方向。现在把 z 方向特别选为沿 方向( 这相当于作一个坐标旋转) , 则的本征值也应为。另外我们知道, 本征值和表象的先取无关。这样选择并不影响结果的普遍性。同理的本征值也都是。我们也能够在为对角矩阵的表象中( 表象) 求本征矢。显然这时的知阵为因此本征矢为注意到本征矢是随着表象选取的不同而改变的。现在是在表象, 而上面算出的表象, 算出的结果应用所不同, 这是下载后可任意编辑合理的。4.在表象中, 求的本征态, 是方向的单位矢。 ( 解) 方法类似前题, 设算符的本征矢是: (1)它的本征值是 。又将题给的算符展开: (2)写出本征方程式: (3)根据问题( 6) 的结论, ,正确共同本征矢, , 运算法则是 , , , , , ( 4) 将这些代入( 3) , 集项后, 对此两边, 的系数: ( 5) 或 下载后可任意编辑( 6) ( 6) 具有非平凡解( 平凡解 , ) 条件是久期方程式为零, 即 它的解 ( 7) 时, 代入( 6) 得: ( 8) (1) 的归一化条件是: 将( 8) 代入( 9) , 得: 归一化本征函数是: ( 10) 时, 的关系是: 归一化本征函数是: ( 11) 下载后可任意编辑是任意的相位因子。本题用矩阵方程式求解: 运用矩阵算符: , , (...