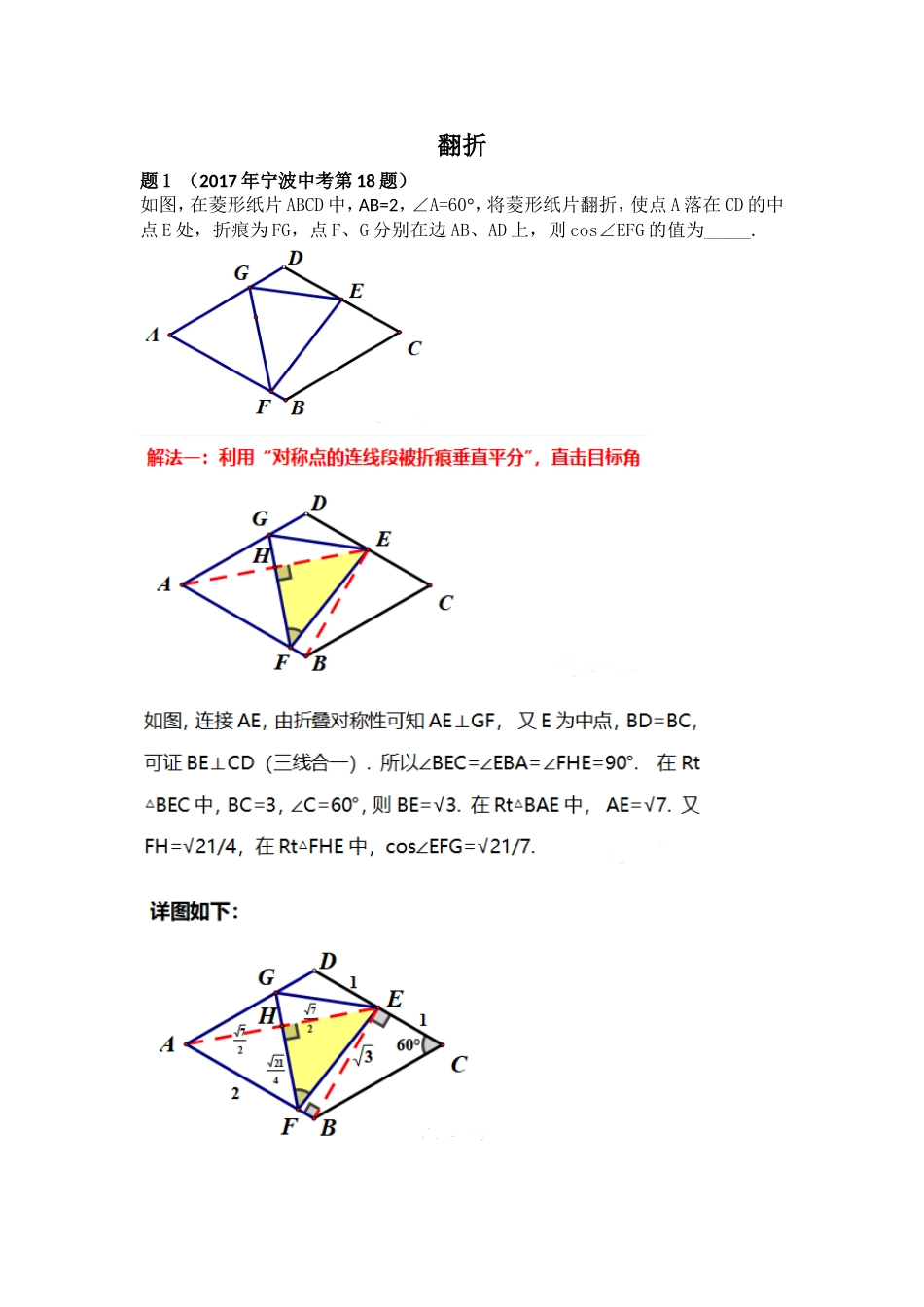
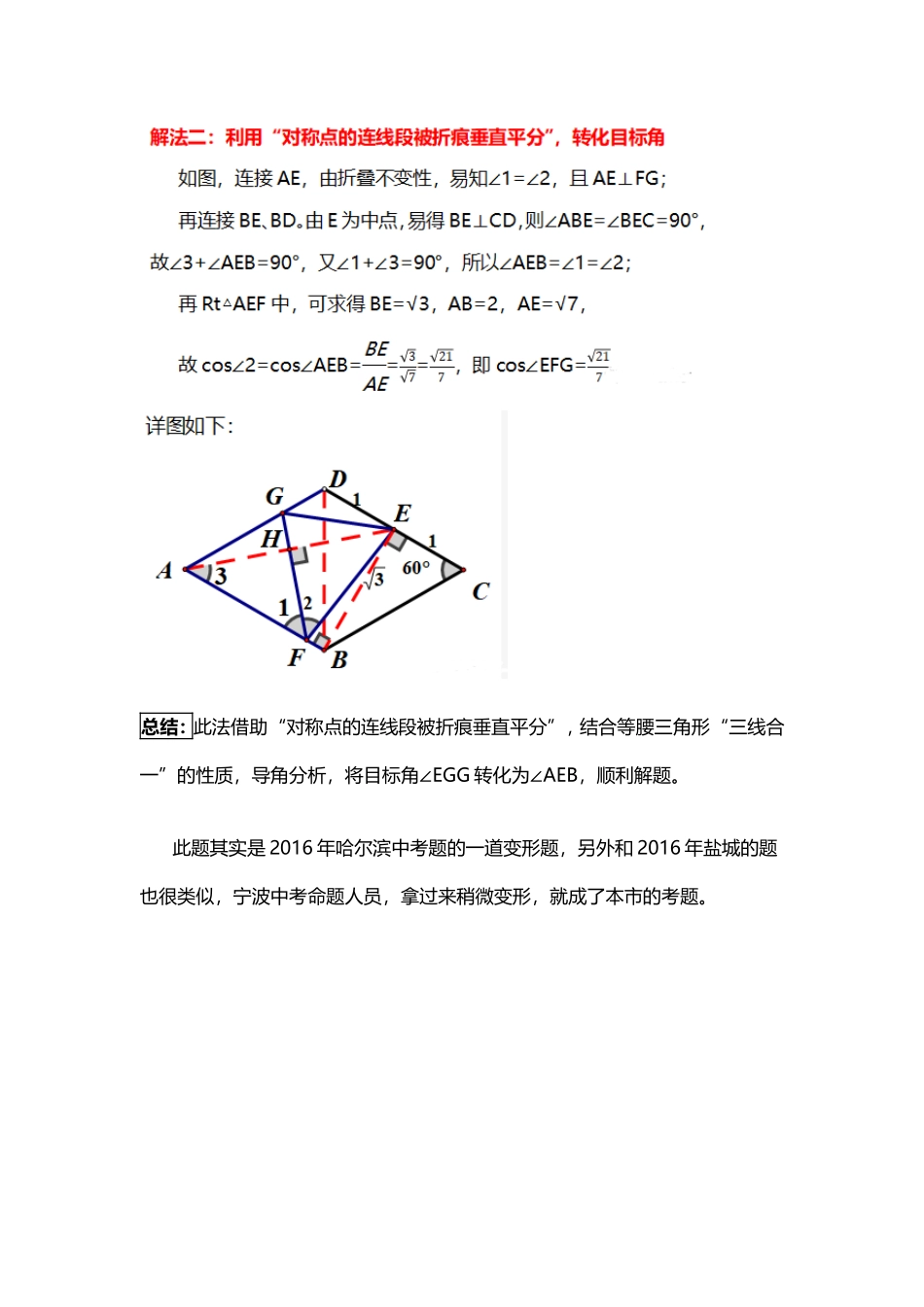
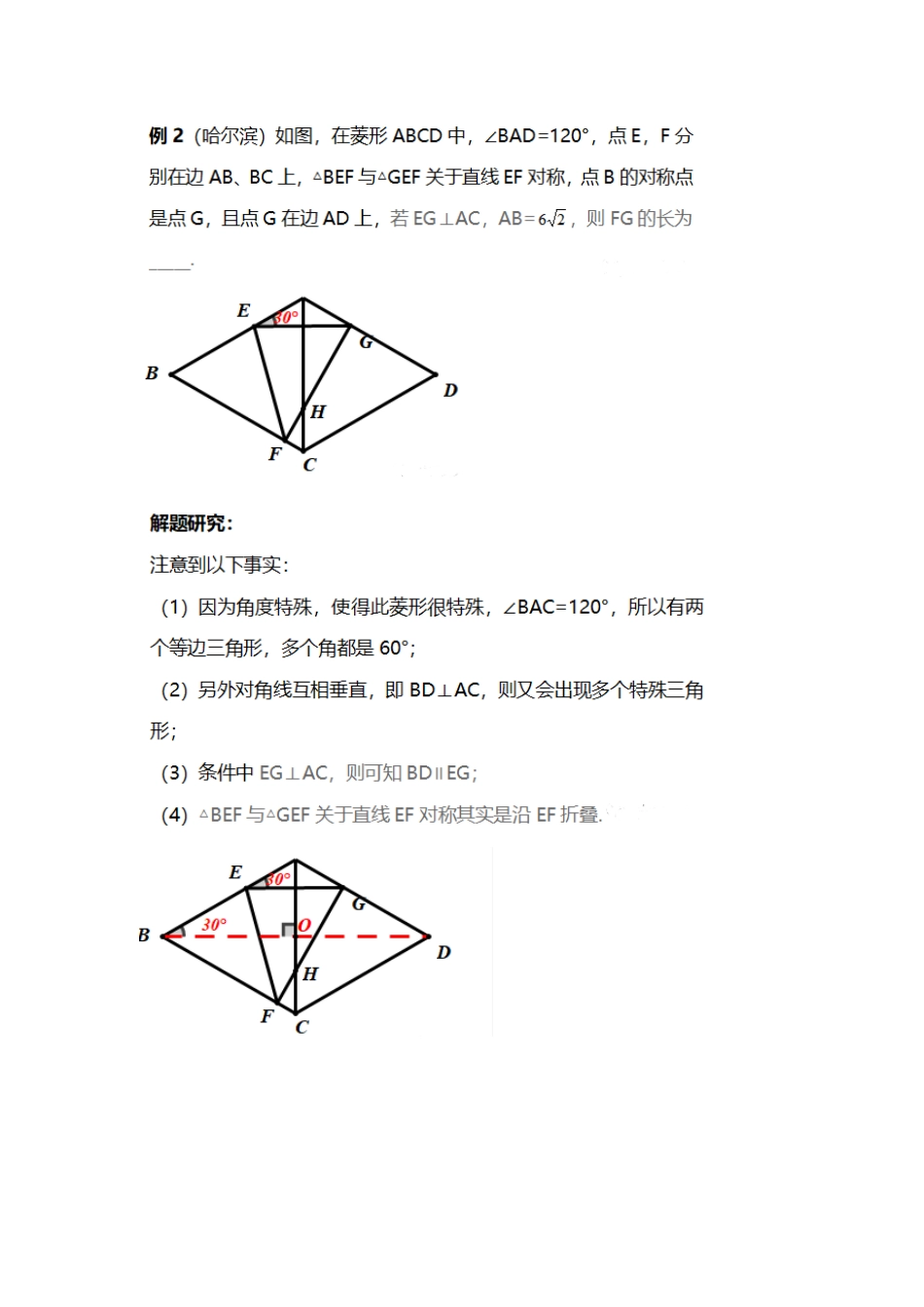
翻折题 1 (2017 年宁波中考第 18 题)如图,在菱形纸片 ABCD 中,AB=2,∠A=60°,将菱形纸片翻折,使点 A 落在 CD 的中点 E 处,折痕为 FG,点 F、G 分别在边 AB、AD 上,则 cos∠EFG 的值为_____.总结:此法借助“对称点的连线段被折痕垂直平分”,结合等腰三角形“三线合一”的性质,导角分析,将目标角∠EGG 转化为∠AEB,顺利解题。此题其实是 2016 年哈尔滨中考题的一道变形题,另外和 2016 年盐城的题也很类似,宁波中考命题人员,拿过来稍微变形,就成了本市的考题。反思:此题关键是发现 FG⊥BC 这一结论,再结合菱形性质解题。此题解法多样,以上三种方法思路自然,尤其是面积法的应用,别具一格,让人眼前一亮!今年镇海区模拟题,也是一道折叠题,题型和以上两题类似,一起来看:变式(2019 镇海模拟)如图,在菱形 ABCD 中,∠A=60°,M、N 分别是边AB、AD 上的两点,将△AMN 沿 MN 翻折,使点 A 恰好与 CD 上的点 A’重合,此时 BD⊥MA’,若折痕 MN=根号 6,则菱形 ABCD 的面积是______.二、矩形中的折叠问题下面看几道矩形中的折叠问题,此类题不难,主要注意的是多种情况的出现:例 3 (直角三角形) 2019 江北区模拟例 4 (等腰三角形)鄞州东钱湖、李关弟、实验中学等校 3 月份模拟总结:以上提供了两种解题方法,法一构造“一线三直角”,再利用相似比进行巧设,最后用勾股定理计算。(其实,注意到∠AFE=90°,那么很容易想到去构造“一线三直角”)!法一很简单,识别中位线模型,借助相似解题。来两道模拟题变式,作为练手用,同学们自行研究三、三角形中的折叠问题由折叠对称性可知,∠1=∠2,已知∠EDC=90°,则∠2+∠3=90°,且∠1+∠4=90°,所以∠3=∠4,得证.总结:此问利用折叠对称后的对应角相等,结合直角三角形,导角分析,完成证明总结:此问求解过程略显复杂,但究其根本是利用折叠不变性,找到了解题的突破口,证明两次全等△BDM△B1DN≅和△ADCMDC≅,得到 AD=DM=DN,再表示出 BN(通过相似△BNEBAC∼),最后通过△END△DAC∼求出 x 的值,利用勾股定理,完美解题。方法总结解决翻折类问题,最核心的是研究翻折前与翻折后的变化,尤其是抓住翻折过程中的不变量——图形全等,从而带来角相等和线段相等等几何元素关系.翻折类问题的思考方式:(1) 观察翻折前后的不变量:对应全等、垂直平分线;(2) 研究翻折后的新图形: 翻折后出现的新图形;(3) 用常见模型解题:如全等勾股、相似等.