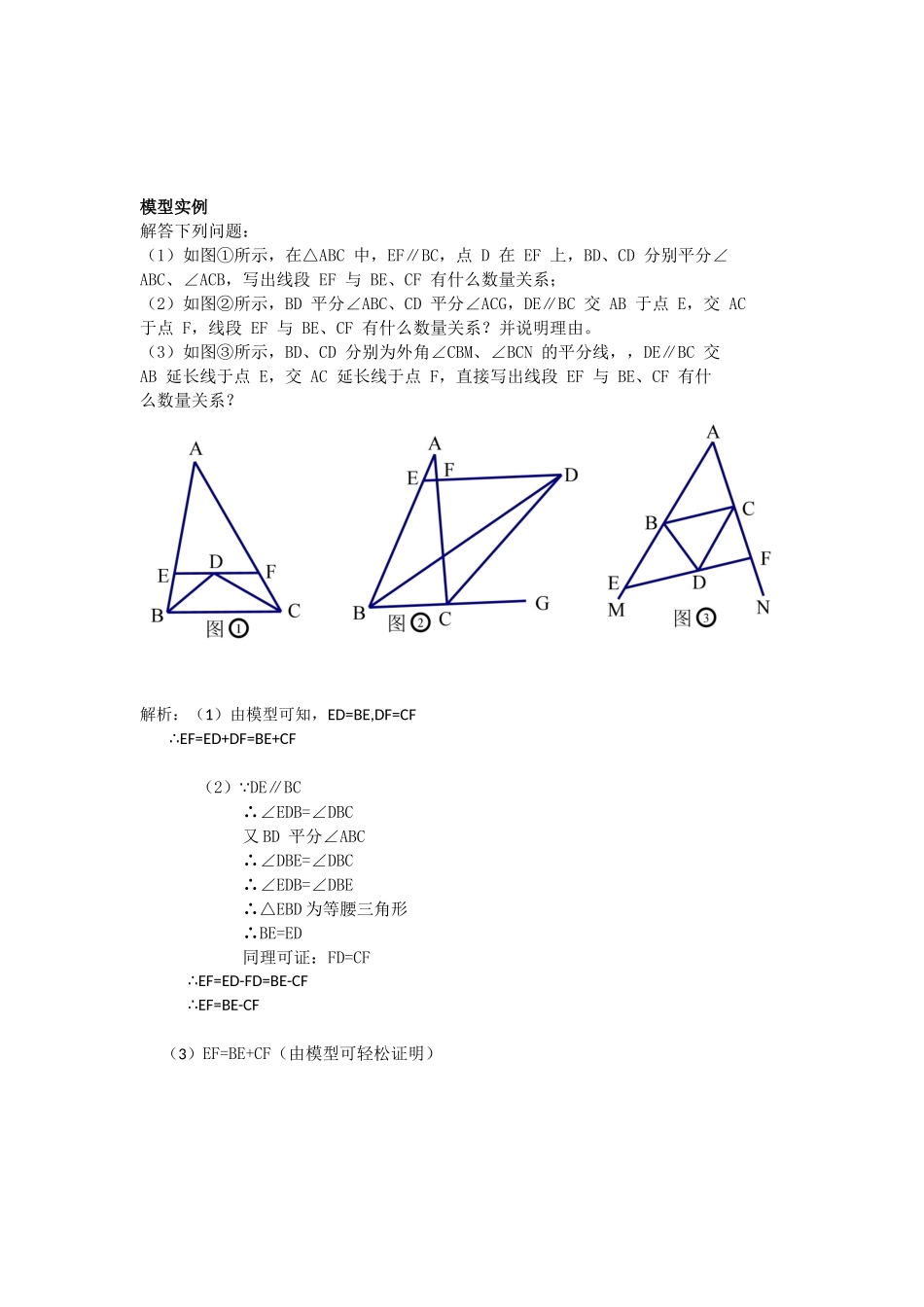
角平分线模型模型 4 角平分线+平行线 如图,P 是∠MON 的平分线上一点,过点 P 作 PQ∥ON,交 OM 于点 Q。 结论:△POQ 是等腰三角形。 模型证明∵PQ∥ON∴∠PON=∠OPQ又∵OP 是∠MON 的平分线∴∠POQ=∠PON∴∠POQ=∠OPQ∴△POQ 是等腰三角形模型分析有角平分线时,常过角平分线上一点作角的一边的平行线,构造等腰三角形,为证明结论提供更多的条件,体现了角平分线与等腰三角形之间的密切关系。 模型实例解答下列问题: (1)如图①所示,在△ABC 中,EF∥BC,点 D 在 EF 上,BD、CD 分别平分∠ ABC、∠ACB,写出线段 EF 与 BE、CF 有什么数量关系; (2)如图②所示,BD 平分∠ABC、CD 平分∠ACG,DE∥BC 交 AB 于点 E,交 AC 于点 F,线段 EF 与 BE、CF 有什么数量关系?并说明理由。 (3)如图③所示,BD、CD 分别为外角∠CBM、∠BCN 的平分线,,DE∥BC 交 AB 延长线于点 E,交 AC 延长线于点 F,直接写出线段 EF 与 BE、CF 有什 么数量关系? 解析:(1)由模型可知,ED=BE,DF=CF EF=ED+DF=BE+CF∴ (2)∵DE∥BC∴∠EDB=∠DBC又 BD 平分∠ABC∴∠DBE=∠DBC∴∠EDB=∠DBE∴△EBD 为等腰三角形∴BE=ED同理可证:FD=CF EF=ED-FD=BE-CF∴ EF=BE-CF∴ (3)EF=BE+CF(由模型可轻松证明)模型练习 1.如图,在△ABC 中,∠ABC、∠ACB 的平分线交于点 E,过点 E 作 MN∥BC,交 AB 于点 M,交 AC 于点 N。若 BM+CN=9,则线段 MN 的长为 。解析:由模型可得,ME=BM,EN=CN MN=ME+EN=∴BM+CN=92.如图,在△ABC 中,AD 平分∠BAC,点 E、F 分别在 BD、AD 上,且 DE=CD,EF=AC求证:EF∥AB。解析:3.如图,梯形 ABCD 中,AD∥BC,点 E 在 CD 上, 且 AE 平分∠BAD,BE 平分∠ABC。 求证:AD=AB-BC。