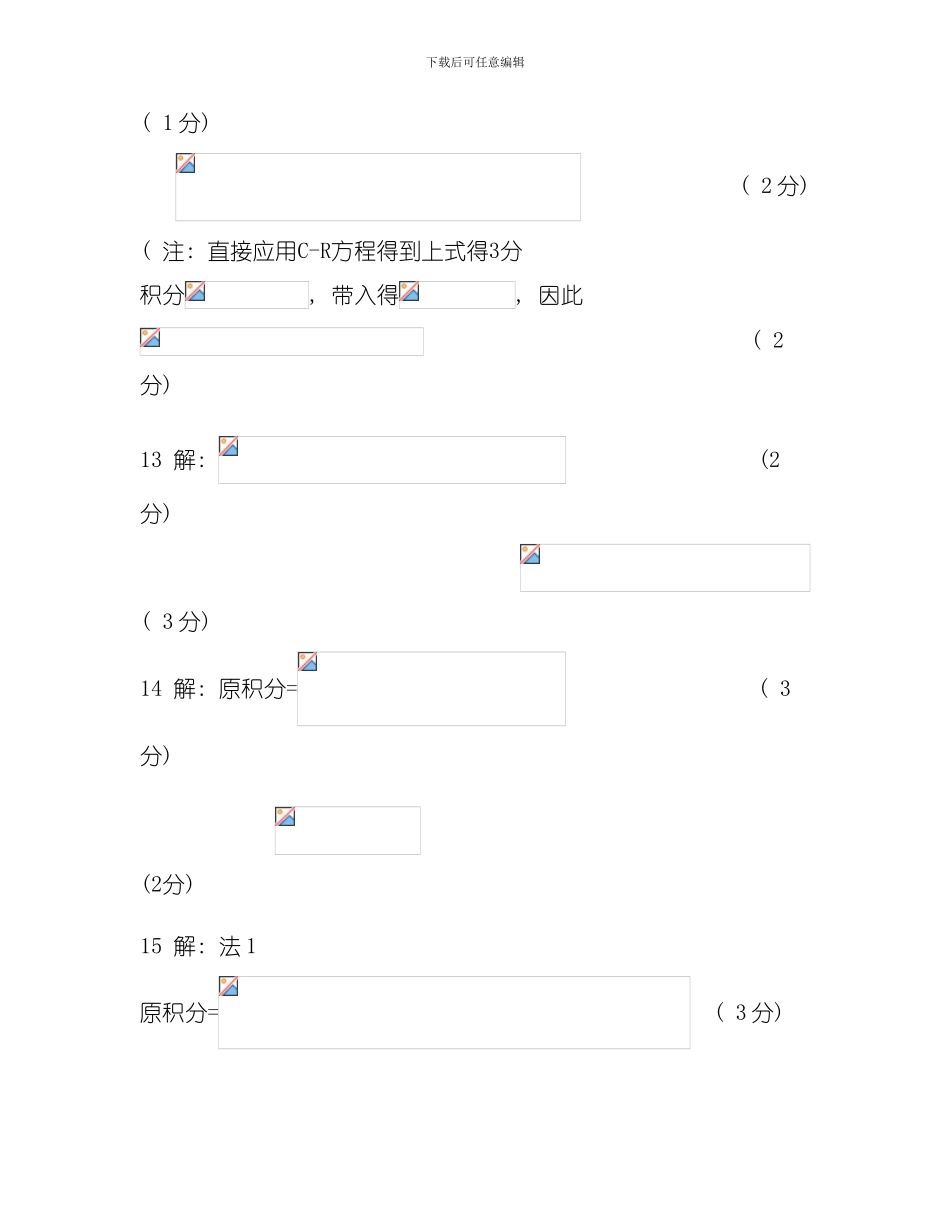
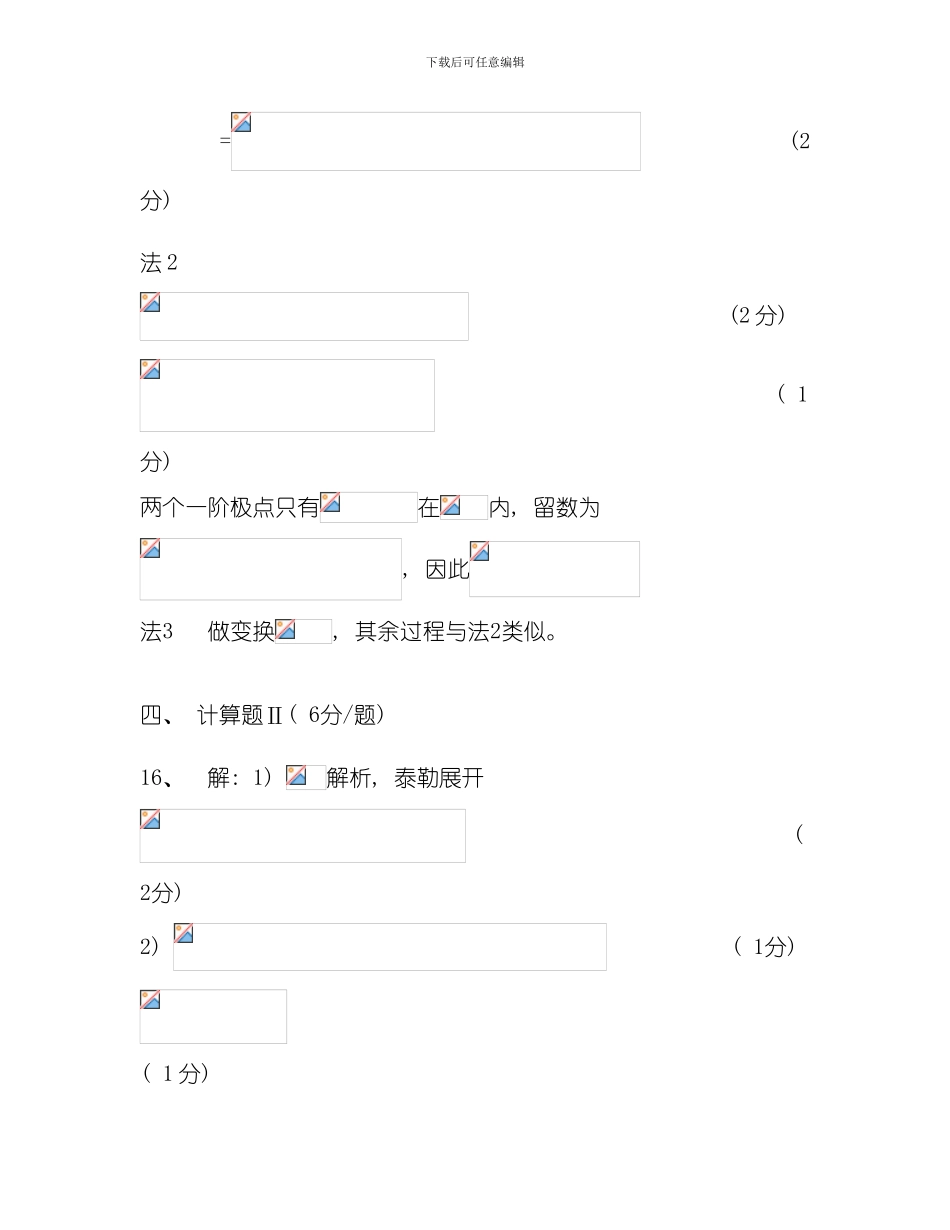
下载后可任意编辑复变函数与积分变换参考答案与评分标准(A卷) -01-04 一、 选择题( 2分/题) 12345DCDAD二、 填空题( 2分/题) 6. 7. 8. 9. 10. 三、 计算题Ⅰ( 5分/题) 11 解: ( 1分) 4 个偏导数均连续( 可微) ( 1 分) 根据 C-R 方程有可导 ( 2分) 不( 无处) 解析 ( 1 分) 12 解: 列出C-R方程 下载后可任意编辑( 1 分) ( 2 分) ( 注: 直接应用C-R方程得到上式得3分积分, 带入得, 因此 ( 2分) 13 解: (2分) ( 3 分) 14 解: 原积分= ( 3分) (2分)15 解: 法 1原积分= ( 3 分) 下载后可任意编辑 = (2分)法 2 (2 分) ( 1分) 两个一阶极点只有在内, 留数为, 因此法3 做变换, 其余过程与法2类似。 四、 计算题Ⅱ( 6分/题) 16、 解: 1) 解析, 泰勒展开 ( 2分) 2) ( 1分) ( 1 分) 下载后可任意编辑3) ( 1 分) ( 1 分) 17 解 1) 当 z=0 时 , ( 2 分) 当 0<|z|<3 时 , 是 二 阶 极 点 , 是 一 阶 极 点 ( 1 分) 当|z|>3 时, 只有在 C 所围内部, ( 1 分) 2) |1|<3, ( 1 分) ( 1 分) 18 解 1) ( 3 分) 2) 下载后可任意编辑 ( 3 分) 五、 应用题(8分) 19 解 设对方程两端取拉式变换, 得: 则 ( 4 分) 利用 ( 2 分) 取反变换得 ( 2 分) 六、 证明题(5+4=9分) 20、 证明: , 故解析 ( 2 分) 利用结论”解析, 则f(z)为常数”, 或者根据C-R方程证明此命题得到结论。 下载后可任意编辑21、 证: (法Ⅰ)令, 则收敛半径, 若 , 得收敛, 与已知矛盾 若,因为收敛, 即在收敛, 则收敛半径, 与假设矛盾。(法Ⅱ)级数收敛, 相当于幂级数在处收敛, 于是由阿贝尔定理, 对于满足的 , 必绝对收敛, 从而该级数的收敛半径; 但若,幂级数在收敛圆内绝对收敛, 特别的在处也绝对收敛, 从而收敛, 与已知矛盾。故的收敛半径为 1。