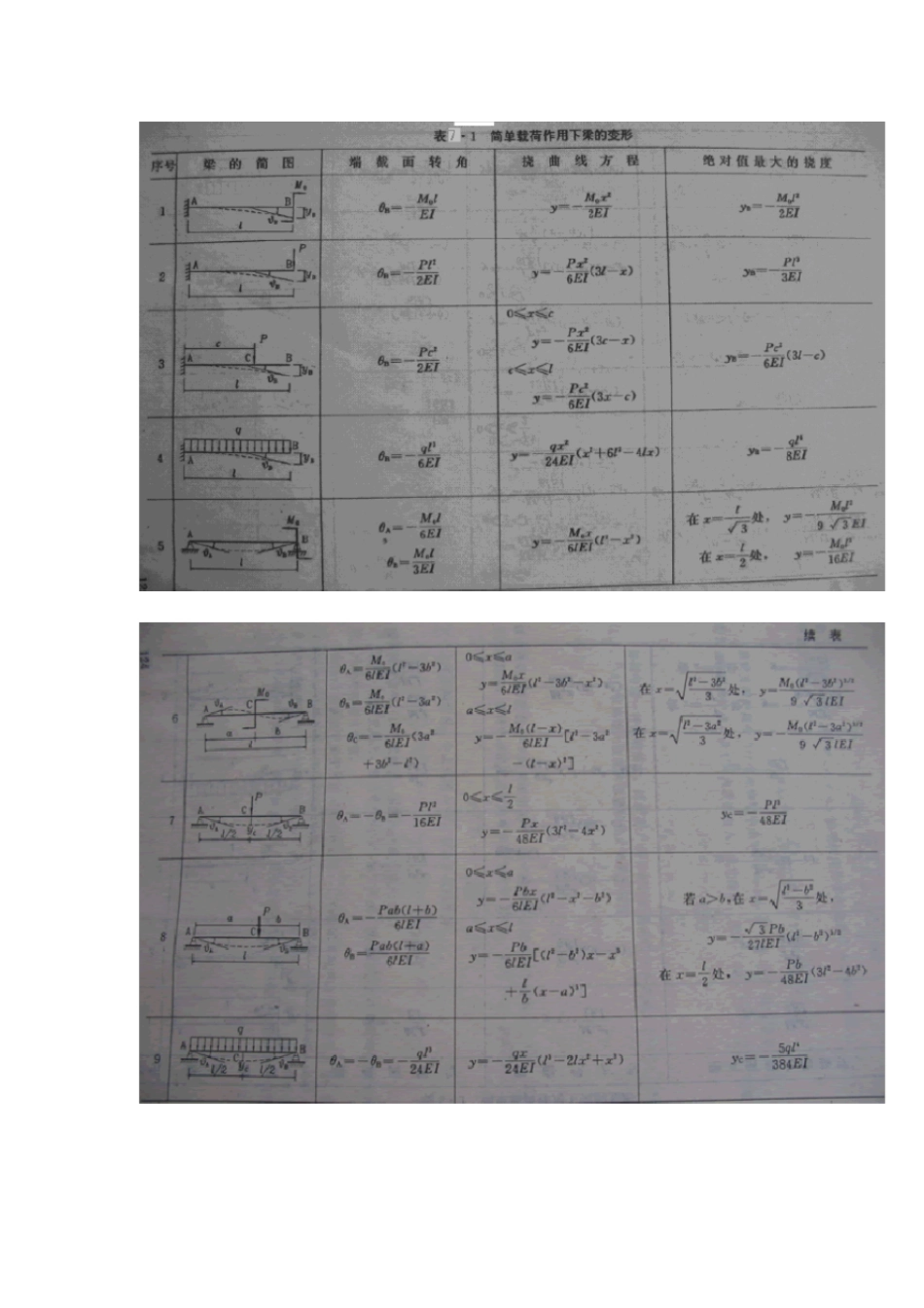
当材料在线弹性范围内工作时,梁的挠度、转角均与载荷成线性关系.而且弯曲变形是很小的.因此,当梁上同时作用几种载荷时,任一载荷引起的变形,不会受到其他载荷的影响,即每种载荷对弯曲变形的影响是各自独立的。所以,几种载荷同时作用下梁的挠度和转角,等于各种载荷单独作用下挠度和转角的代数和,这就是求解弯曲变形的叠加法.当只需确定某些指定截面的挠度和转角时,应用叠加法是比较方便的.下面举例说明.例 7-3 图 7-8 所示简支梁,承受均布载荷q 和集中力偶M 0 作用,已知M0 =ql2 。试求跨度中点的挠度 f c 和 A 截面的转角θA 。解:利用叠加法求解时,首先将q , M 0 同时作用下的简支梁( 图 7 -8a ) ,分解为q 作用下的简支梁( 图 7-8b) 和 M 0 作用下的简支梁( 图 7 -8c ) ,然后,由表7.1 查取结果叠加。从表的第9 栏查得均布载荷q 作用下的中点挠度和A 端面转角分别为由表 7.1 第 5 栏查得集中力偶M0 作用下的中点挠度和A 端面转角分别为叠加以上结果,求得q , M 0 同时作用下的中点挠度和A 截面转角为f c 为负值,表示挠度向下.θ A 为负值,表示A 截面顺时针转动.例 7-4 简支梁如图7 — 10a 所示,在2a 的长度上对称地作用有均布载荷q. 试求梁中点挠度和梁端面的转角.解:利用叠加法求解。由于简支梁上的载荷对跨度中点C 对称,故C 截面的转角应为零.因而从C 截面取出梁的一半,可将其简化为悬臂梁,如图7 — 10b 所示。梁上作用有均布载荷q 和支座B 的反力RB = qa. 这样,悬臂梁上B 端面的挠度在数值上等于原梁中点C 的挠度,但符号相反,B 端面的转角即为原梁B 端面的转角.经这样处理后,应用叠加原理求解比较方便.由表 7 · 1 的第2 栏查得,当集中力RB (=qa) 作用时( 图 7 — 10c ) , B 端面的转角和挠度分别为由表 7 · 1 的第4 栏查得,当均布载荷q 作用时( 图 7 — 10d) , E 截面的转角和挠度分别为由于 EB 梁段上无载荷作用,所以q 引起 B 点的转角和挠度分别为= = 叠加上述结果,可得B 端面的转角和挠度分别为于是,原梁( 图 7 — 10a ) 中点 C 的挠度f c 为例 7-6 某一变截面外伸梁如图7 — 11a 所示. AB 、 BC 段的抗弯刚度分别为EI 1 和 EI 2 ,在 C 端面处受集中力P 作用,求C 端面的挠度和转角.解:由于外伸梁是变截面的,故不能直接应用表7 . 1...