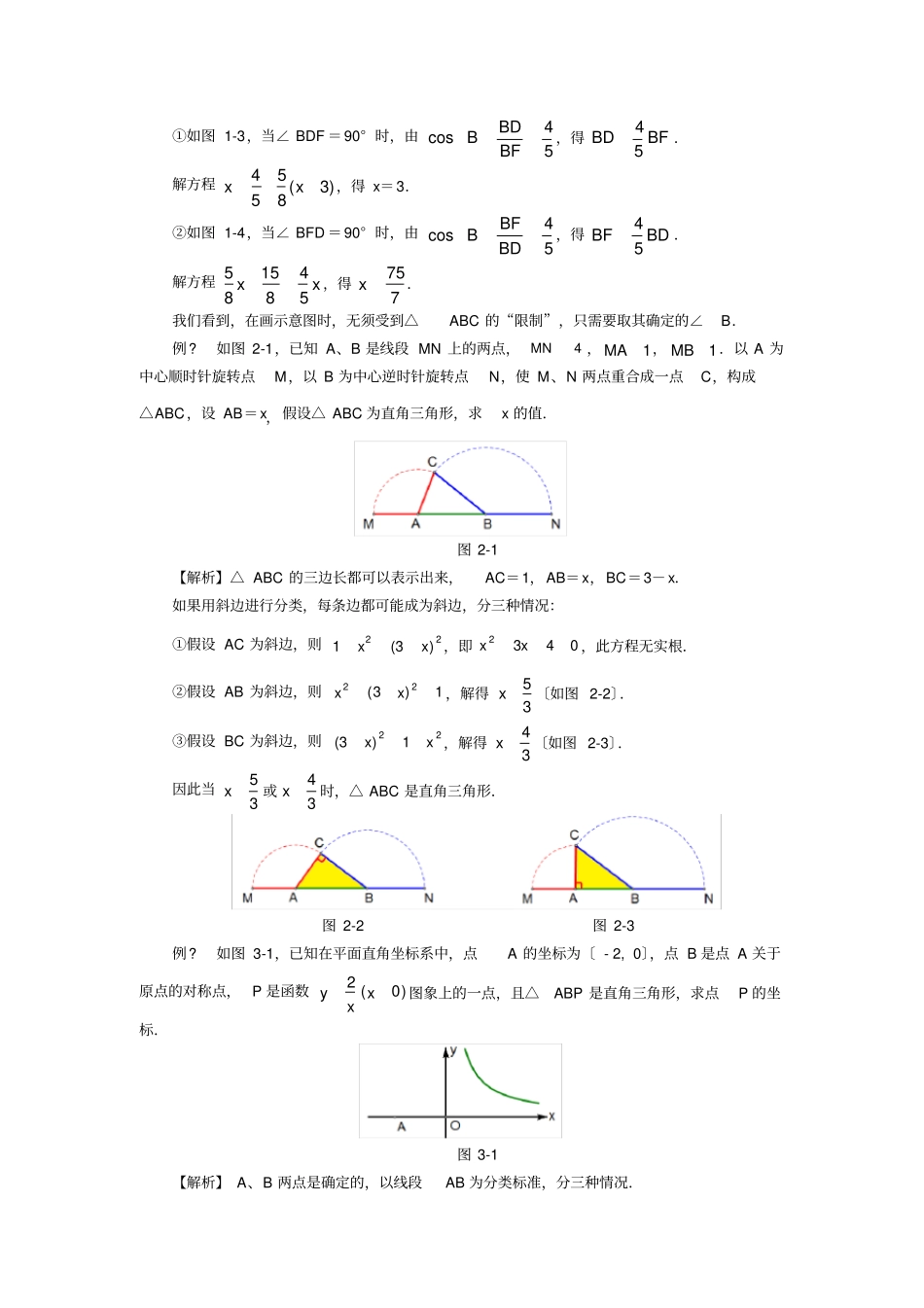
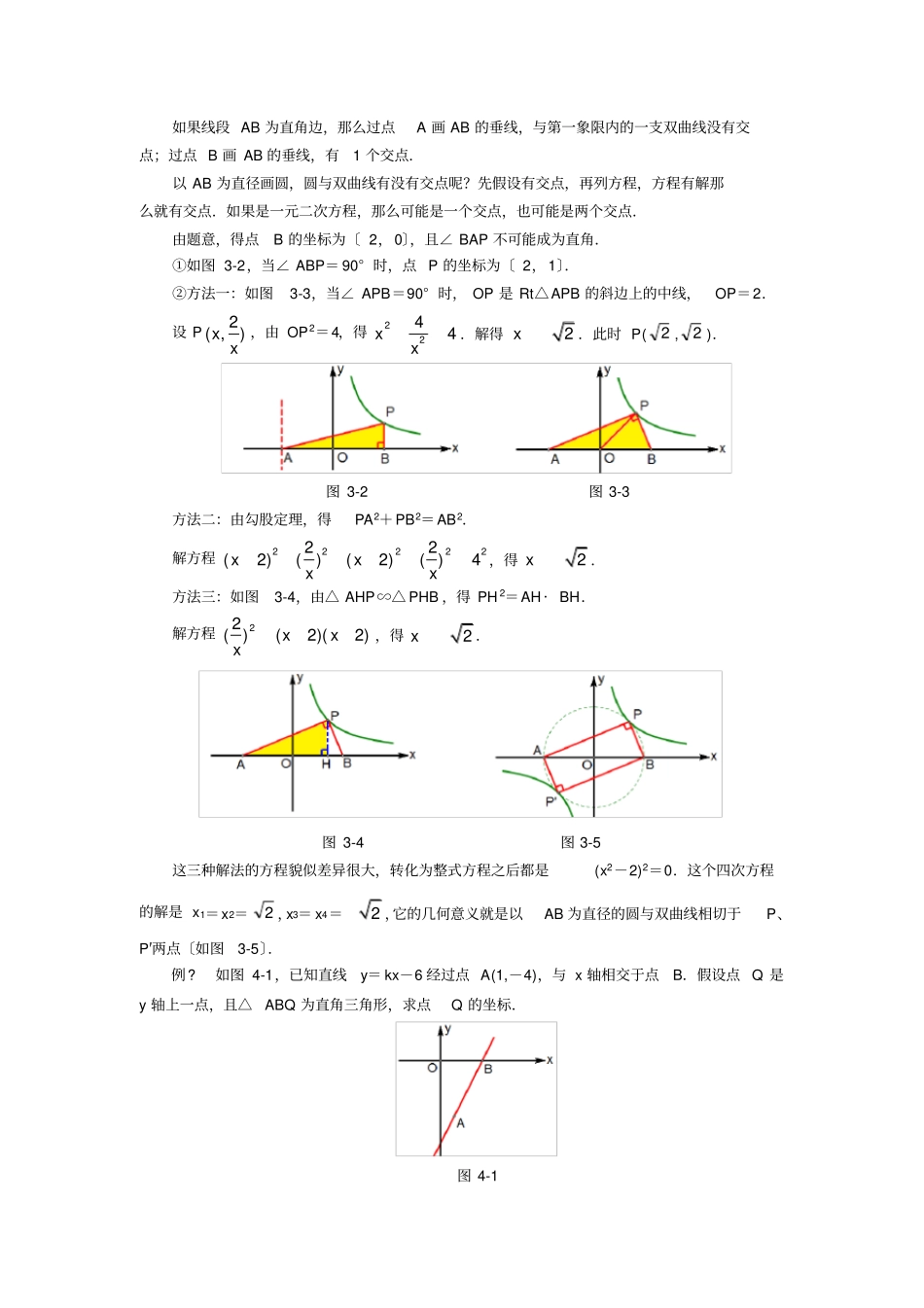
中考数学压轴题解题策略〔3〕直角三角形的存在性问题解题策略《挑战压轴题· 中考数学》的作者上海 马学斌专题攻略解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.在平面直角坐标系中,两点间的距离公式常常用到.怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边, 那么以斜边为直径画圆,直角顶点在圆上〔不含直径的两个端点〕.例题解析例?如图 1-1,在△ ABC 中, AB= AC=10, cos∠B= 45.D、E 为线段 BC 上的两个动点,且 DE=3〔E 在 D 右边〕,运动初始时D 和 B 重合, 当 E 和 C 重合时运动停止.过E作 EF//AC 交 AB 于 F,连结 DF.设 BD=x,如果△ BDF 为直角三角形,求x 的值.图 1-1 【解析】△ BDF 中,∠ B 是确定的锐角,那么按照直角顶点分类,直角三角形BDF 存在两种情况. 如果把夹∠ B 的两条边用含有x 的式子表示出来, 分两种情况列方程就可以了.如图 1-2,作 AH⊥BC,垂足为 H,那么 H 是 BC 的中点.在 Rt△ABH 中, AB= 10,cos∠ B= 45,所以 BH=8.所以 BC=16.由 EF//AC,得 BFBEBABC,即31016BFx.所以 BF= 5 (3)8x.图 1-2 图 1-3 图 1-4 ①如图 1-3,当∠ BDF =90° 时,由4cos5BDBBF,得45BDBF .解方程45(3)58xx,得 x=3.②如图 1-4,当∠ BFD =90° 时,由4cos5BFBBD,得45BFBD .解方程 5154885xx ,得757x.我们看到,在画示意图时,无须受到△ABC 的“限制”,只需要取其确定的∠B.例?如图 2-1,已知 A、B 是线段 MN 上的两点,,,.以 A 为中心顺时针旋转点M,以 B 为中心逆时针旋转点N,使 M、N 两点重合成一点C,构成△ABC,设 AB=x,假设△ ABC 为直角三角形,求x 的值.图 2-1 【解析】△ ABC 的三边长都可以表示出来,AC=1,AB=x,BC=3-x.如果用斜边进行分类,每条边都可能成为斜边,分三种情况:①假设 AC 为斜边...