方波信号的分解与合成

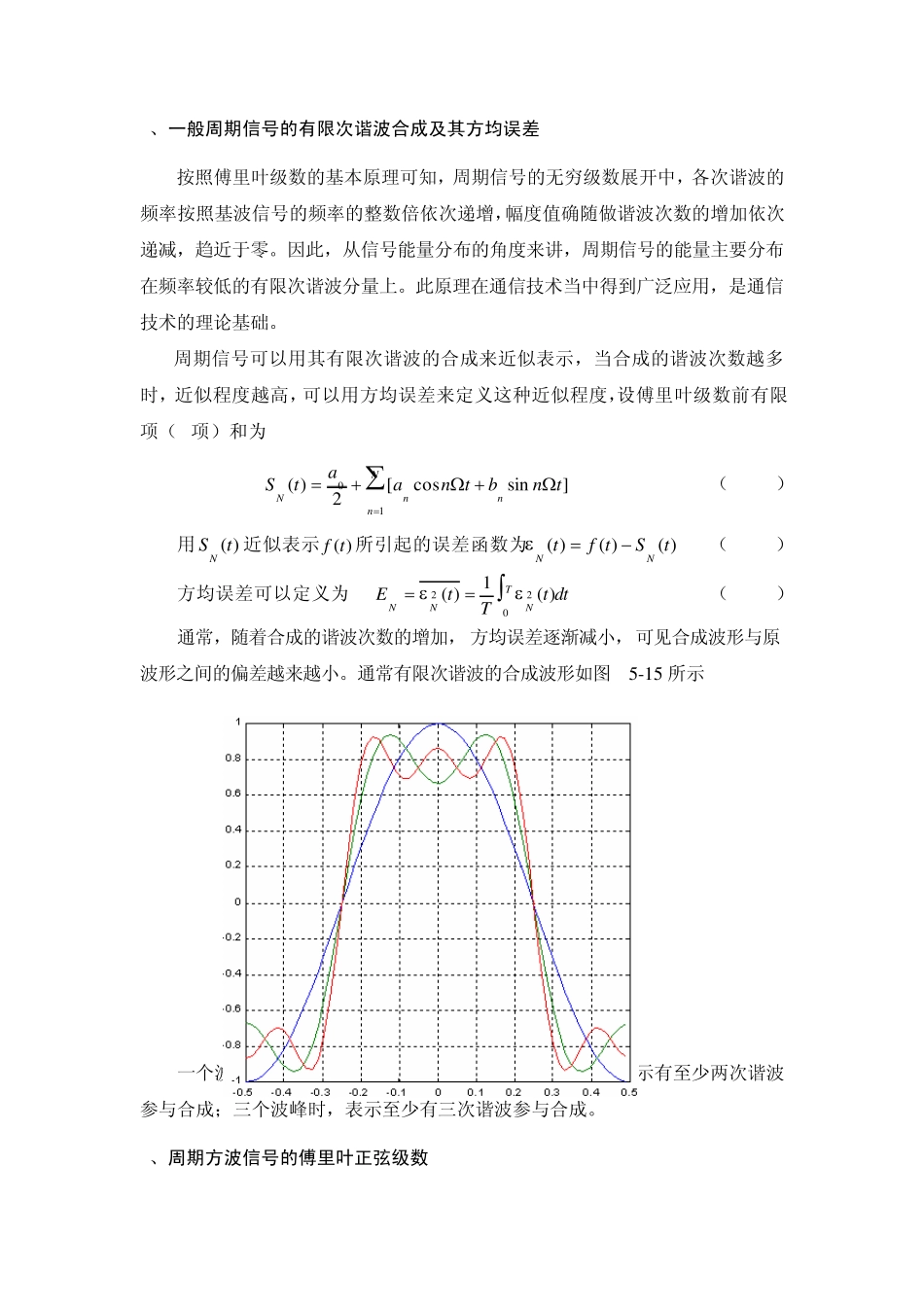
实验四 方波信号的分解与合成 任何电信号都是由各种不同频率、幅度和初相的正弦波迭加而成的。1822年法国数学家傅里叶在研究热传导理论时提出并证明了将周期函数展开为正弦级数的原理。奠定了傅里叶级数的理论基础、揭示了周期信号的本质，即任何周期信号（正弦信号除外）都可以看作是由无数不同频率、不同幅度的正弦波信号叠加而成的，就像物质都是由分子或者原子构成一样。周期信号的基本单元信号是正弦谐波信号。 一、实验目的 1、通过对周期方波信号进行分解，验证周期信号可以展开成正弦无穷级数的基本原理，了解周期方波信号的组成原理。 2、测量各次谐波的频率与幅度，分析方波信号的频谱。 3、观察基波与不同谐波合成时的变化规律。 4、通过方波信号合成的实验，了解数字通信中利用窄带通信系统传输数字信号（方波信号）的本质原理。 二、实验原理 1、一般周期信号的正弦傅里叶级数 按照傅里叶级数原理，任何周期信号在满足狄利克雷条件时都可以展开成如式 2-3-1 所示的无穷级数 10110)cos(2)sin()cos(2)(nnnnnnntnAAtnbtnaatf （2-4-1） 其中)cos(nntnA称为周期信号的n谐波分量，n次谐波的频率为周期信号频率的 n倍，每一次的谐波的幅度随谐波次数的增加依次递减。当0n时的谐波分量为 20a （直流分量）。当1n时的谐波分量为)cos(11tA（一次谐波或基波分量直流分量）。 2、一般周期信号的有限次谐波合成及其方均误差 按照傅里叶级数的基本原理可知，周期信号的无穷级数展开中，各次谐波的频率按照基波信号的频率的整数倍依次递增，幅度值确随做谐波次数的增加依次递减，趋近于零。因此，从信号能量分布的角度来讲，周期信号的能量主要分布在频率较低的有限次谐波分量上。此原理在通信技术当中得到广泛应用，是通信技术的理论基础。 周期信号可以用其有限次谐波的合成来近似表示，当合成的谐波次数越多时，近似程度越高，可以用方均误差来定义这种近似程度，设傅里叶级数前有限项（N项）和为 ]sincos[2)(10tnbtnaatSnNnnN （2-4-2） 用)(tSN近似表示)(tf所引起的误差函数为)()()(tStftNN （2-4-3） 方均误差可以定义为 dttTtETNNN022)(1)( （2-4-4） 通常，随着合成的谐波次数的增加，方均误差逐渐减小，可见合成波形与原波形之间的偏差越来越小。通常有限次谐波的合成波形如图5-15 所示 图 5-15 方波信号有限次谐...