泰勒公式的物理意义VIP专享

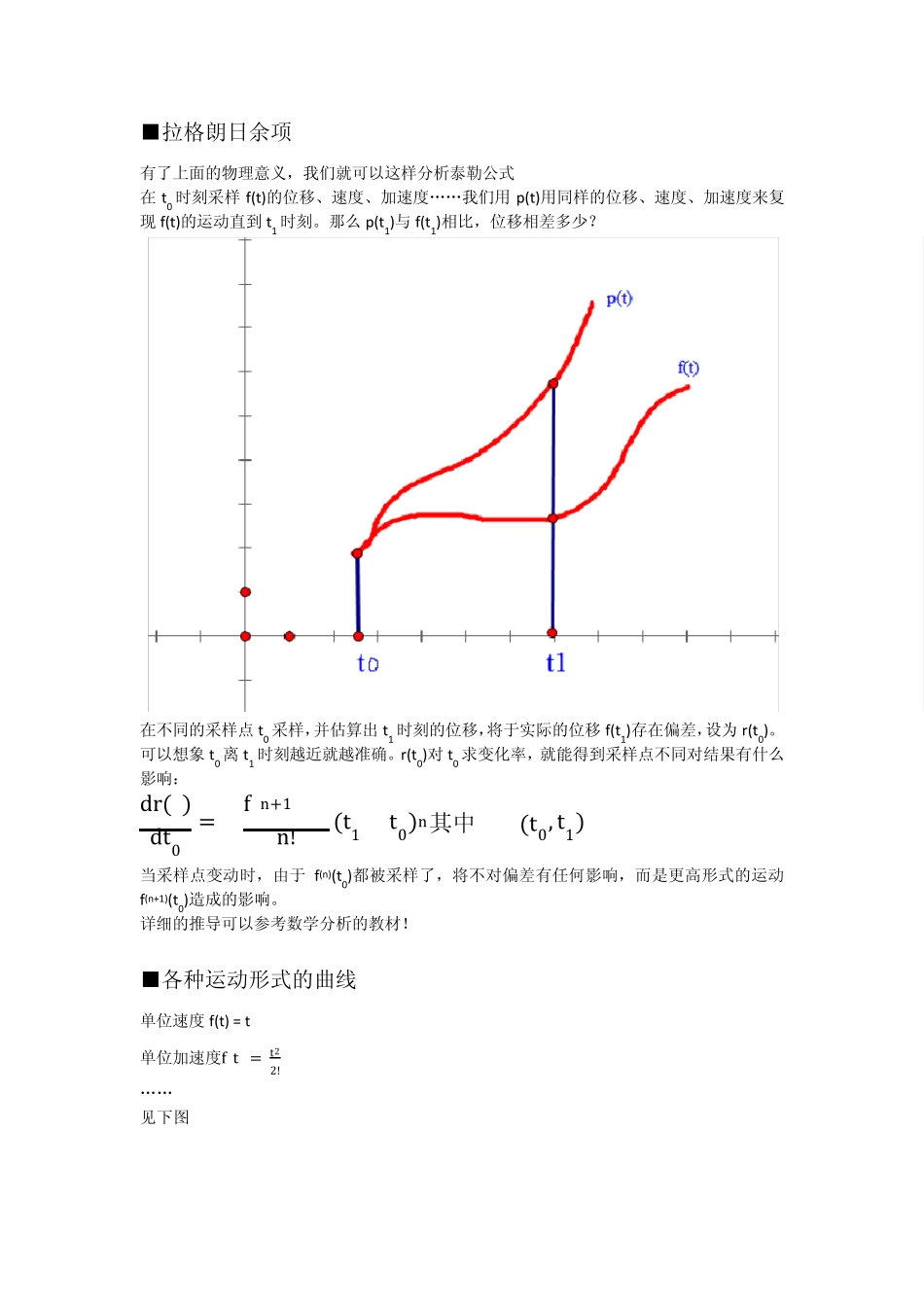
泰勒公式 ■下面的图形在 0 点附近多么相似： ■泰勒公式的由来： 下面对教科书中为什么不使用 n 次罗比达法则进行说明： 令r x = f 0 a0 + f ′ 0 a1 + f ′′ 0 a2 + …+ f n 0 an −f(x) 其中an = xnn! 求 时使用罗比达法则，分子分母求 n 次导得 limx→0r(x)xn = limx→0f n 0 −f n (x)n! 问题是 f(x)在 0 点处是不是 n 阶可导并连续。如果连续那么上式的极限存在并为 0，如果不连续那么不可以用这种方法求出这个极限。教科书上都利用到 n-1 次罗比达法则，最后利用n 次可导。 ■物理意义： 可以想象函数 f(t)表达了物体的位移(从青岛开往北京的火车?) 假设知道了 初始位移 s0 初始速度 v 初始加速度 a 那么多项式p t = s0 + vt + at22! p(t)与 f(t)至少在初始位置，位移、速度、加速度都一样，未来呢？ 火车 f(t)驶过家门，只捕捉到了它的一瞬间，之后只能猜测它是以 p(t)运行了 ■拉格朗日余项 有了上面的物理意义，我们就可以这样分析泰勒公式 在t0 时刻采样f(t)的位移、速度、加速度……我们用 p(t)用同样的位移、速度、加速度来复现 f(t)的运动直到 t1 时刻。那么 p(t1)与 f(t1)相比，位移相差多少？ 在不同的采样点 t0 采样，并估算出 t1 时刻的位移，将于实际的位移f(t1)存在偏差，设为 r(t0)。可以想象 t0 离 t1 时刻越近就越准确。r(t0)对 t0 求变化率，就能得到采样点不同对结果有什么影响： dr(ε)dt0= −f n+1 ε n!(t1 −t0)n其中 ε∈(t0, t1) 当采样点变动时，由于 f(n)(t0)都被采样了，将不对偏差有任何影响，而是更高形式的运动f(n+1)(t0)造成的影响。 详细的推导可以参考数学分析的教材！ ■各种运动形式的曲线 单位速度f(t) = t 单位加速度f t = t22! …… 见下图 图中可以发现，越高级的运动形式在短时间不会有很大的作用，不过时间长了影响会非常剧烈。 ■拉格朗日余项的物理解释 这里先把公式清楚的写出来: f t = f t0 + f ′ t0 t−t0 + ……+ f n t0 n!(t−t0)n + f n+1 ε (n + 1)! (t−t0)n 左侧 f(t)是本来的运动 右侧f t0 + f ′ t0 t−t0 + ……+ f n t0 n!(t−t0)n是估计的运动 二者在t时刻的位移相差f n+1 ε n+1 ! (t−t0)n+1 ，这是我们忽略的更高层次的运动形式 例如： f(t) = 1 + t p(t) = 1 位移偏差的原因是由速度引起的，因为 p(t)没有考虑速度的因素 f t = 1 + t + t22! p(t) = 1 + t 位移产生的偏差是由加速度引起的，因为p(t)并没有考虑加速度 ■更进一步 如果采样点变多，逼近多项式p(t)将使用拉格拉日差值多项式，泰勒公式只能在局部使用，因为高阶的运动很快将发挥作用，极大地影响了位移的估计结果。