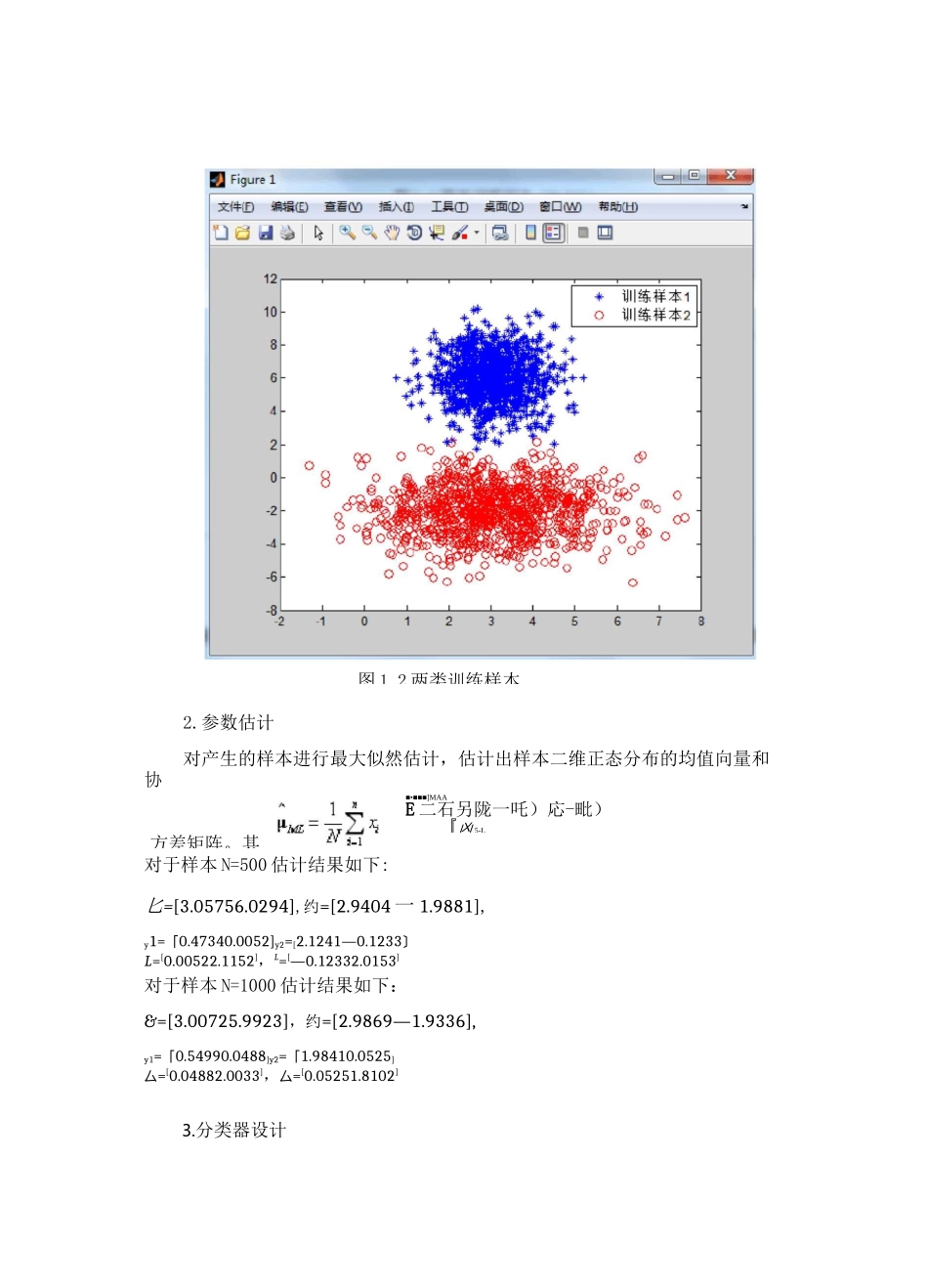
二、实验原三、其中,u-[3,6]T,L-110.50「02,u-[3,-2]T,L 二11、实验目的1. 掌握密度函数监督参数估计方法;2. 掌握贝叶斯最小错误概率分类器设计方法。贝叶斯分类器是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。它的设计方法是一种最基本的统计分类方法。其分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。对于两类分类问题,已知先验概率 P(«1)和 P(®2),以及类别标号和®2,得到相应的类条件概率密度 P(x|®1),P(X®2),由贝叶斯公式:八 IP(尤血 i)F3)计算得到条件概率 P(3i|x)(i=],2),又称为后验概率。如果:Pg|x)=maxPg|x),xG叫或者:P(®]|x)>P(®2|x),XG3]P(®2|x)>P(3]|x),XG32实验内容对于一个两类分类问题,设两类的先验概率相同(P(O)二 P(O)),两类的 12类条件概率密度函数服从二维正态分布,即P(xI①)〜N(u,L)P(xI①)〜N(u,远)1112221•生成两类模式随机样本点并进行分类;2.设计最大似然估计算法对两类类条件概率密度函数进行估计3.用 2 中估计的类条件概率密度函数设计最小错误概率贝叶斯分类器,实现对两类样本的分类。四、实验步骤1.产生训练样本根据实验提供的先验均值向量和协方差矩阵,利用编写的multivrandn 函数构造二维正态分布,分别产生 N=500 及 N=1000 个样本,所得结果如图 1.1 及 1.2 所示。图 1.1 两类训练样本(N=500)方差矩阵。其2.参数估计对产生的样本进行最大似然估计,估计出样本二维正态分布的均值向量和协对于样本 N=500 估计结果如下:匕=[3.05756.0294],约=[2.9404 一 1.9881],y1=「0.47340.0052]y2=[2.1241—0.1233〕L=[0.00522.1152],L=[—0.12332.0153]对于样本 N=1000 估计结果如下:&=[3.00725.9923],约=[2.9869—1.9336],y1=「0.54990.0488]y2=「1.98410.0525]厶=[0.04882.0033],厶=[0.05251.8102]3.分类器设计图 1.2 两类训练样本■•■■■]MAAE 二石另陇一吒)応-毗)『凶 5-L根据上面得出的参数估计结果和贝叶斯最大后验概率判决准则设计分类器当,则。设计分类函数,对样本进行分类判决。例如对类别 1 中的第一个样本进行分类,结果如图 2 所示:feiilei(samples1(:)ppwl5pw2^u_15sigljsig25d)样本属于第一类""f 匹»图 2.分类结果对两组样本进行分类,运用 matlab 理论分别计算出 N=500 及 N=1000 个样本的分...