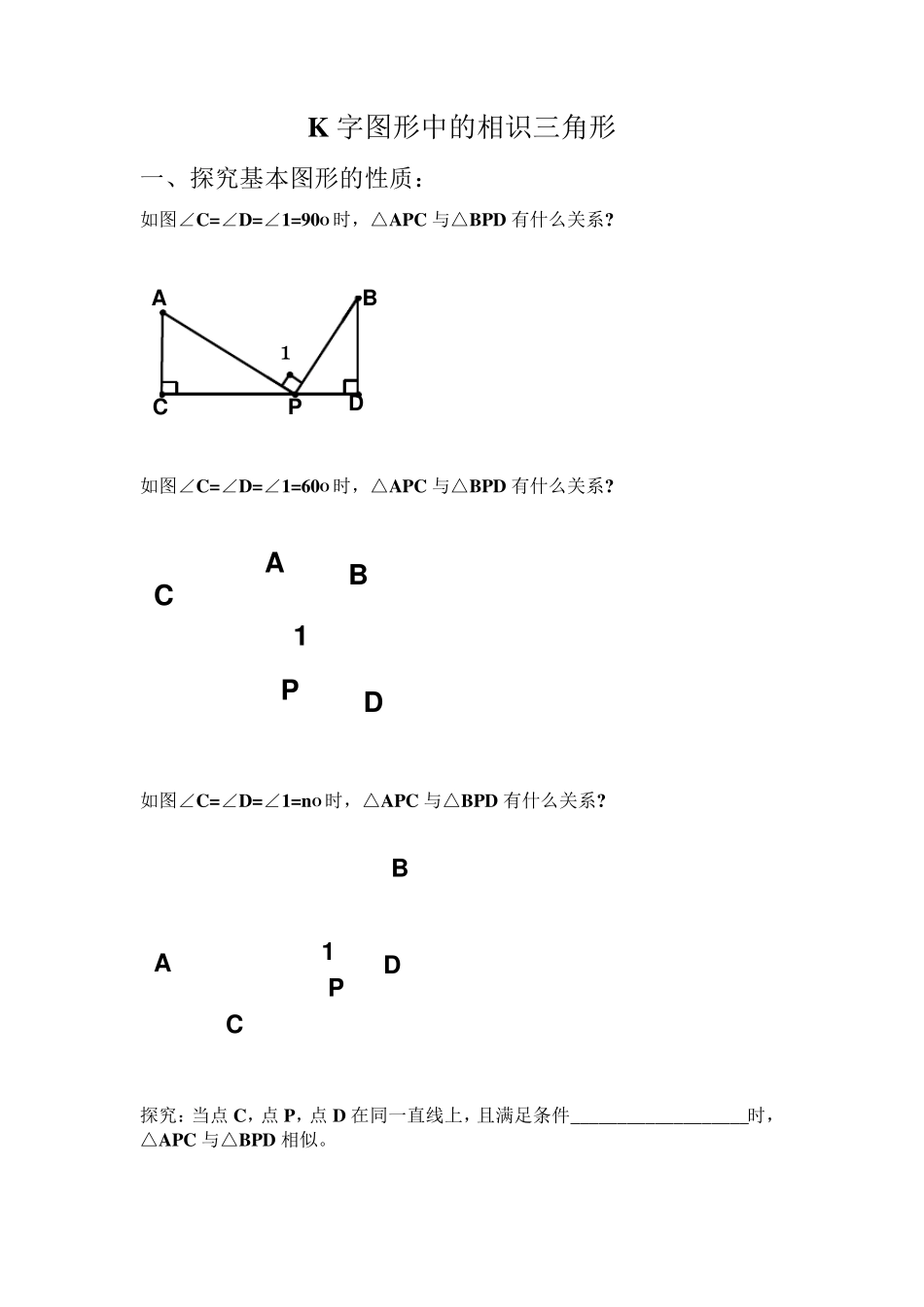
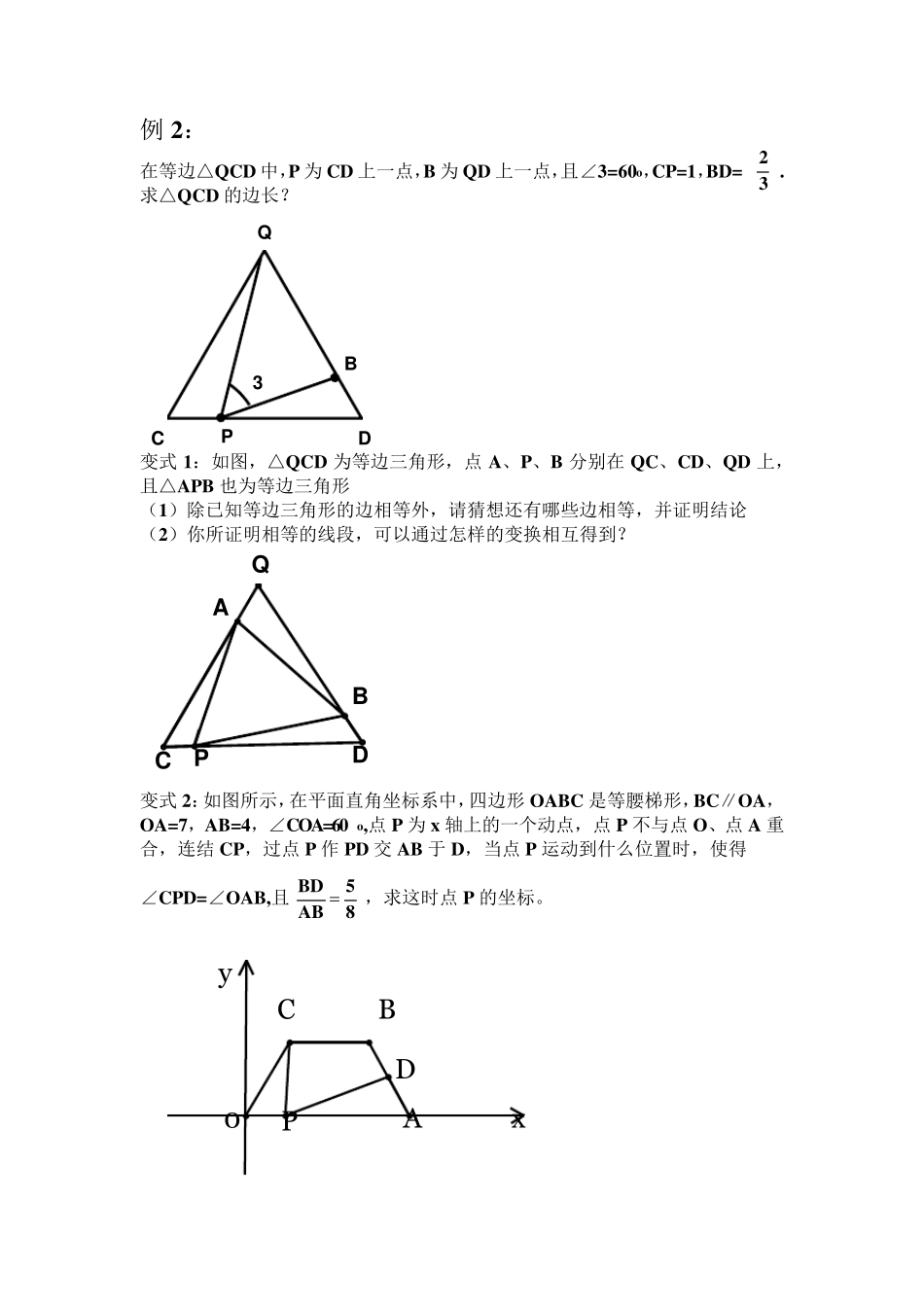
K 字图形中的相识三角形 一、探究基本图形的性质: 如图∠C=∠D=∠1=90O 时,△APC 与△BPD 有什么关系? 如图∠C=∠D=∠1=60O 时,△APC 与△BPD 有什么关系? 如图∠C=∠D=∠1=nO 时,△APC 与△BPD 有什么关系? 探究:当点 C,点 P,点 D 在同一直线上,且满足条件___________________时,△APC 与△BPD 相似。 A C D 1 P B 1 B A C D P D 1 B A C P 二、基本图形的应用: 例 1: 在矩形 ABCD 中,AB=10,AD=8,F 是 CD 上一动点,沿 EF 折叠后,点 C 恰好落在 AB 上 G 处,E 在 BC 上 (1)F 与 D 重合时,求折痕 EF 的长 (2)BG=6 时,能求折痕 EF 的长吗? (3)试求 BG 的取值范围 突破题(课后完成): (4)F 与 D 重合时,是否存在过点 G 的直线 L、直线 DE 与 x轴所围成的三角形和直线 L、直线 DE 与 y轴所围成的三角形相似,如果存在,请直接写出解析式,并画出相应的直线;如果不存在请说明理由. EFCBAQGECBAD(F)GECBAD(F)G例2: 在等边△QCD 中,P 为CD 上一点,B 为QD 上一点,且∠3=60o,CP=1,BD= . 求△QCD 的边长? 变式 1:如图,△QCD 为等边三角形,点A、P、B 分别在QC、CD、QD 上,且△APB 也为等边三角形 (1)除已知等边三角形的边相等外,请猜想还有哪些边相等,并证明结论 (2)你所证明相等的线段,可以通过怎样的变换相互得到? 变式 2:如图所示,在平面直角坐标系中,四边形 OABC 是等腰梯形,BC∥OA,OA=7,AB=4,∠COA=60 o,点P 为x轴上的一个动点,点P 不与点O、点A 重合,连结 CP,过点P 作 PD 交 AB 于 D,当点P 运动到什么位置时,使得 ∠CPD=∠OAB,且 ,求这时点P 的坐标。 32Q C D P B 3 85ABBD C B A D P Q y x 0 B C A P D 作业: 已知:等腰梯形ABCD 中,AB∥CD,AB<CD, AB=10,BC=3 (1)如图,点M 为AB 上一点,且满足∠1=∠A,求 AM 的长; (2)如图,点M 在 AB 上移动(M 不与 A、B 重合),且满足 ∠1=∠A,MN 交 BC 的延长线于点N,设 AM=x,CN=y,求 y关于 x的函数关系式? B M A C D N C A B D M 练习: 1、已知:QC=QD=2,∠C=∠D=∠3=45o,P 在 CD 上运动不与 C、D 重合,设CP=x,QB=y,求 y关于 x的函数关系式 变式:若 QC=QD=2,∠C=45o=∠3,点 P 在 CD 的中点处,∠3 绕中点旋转,∠...