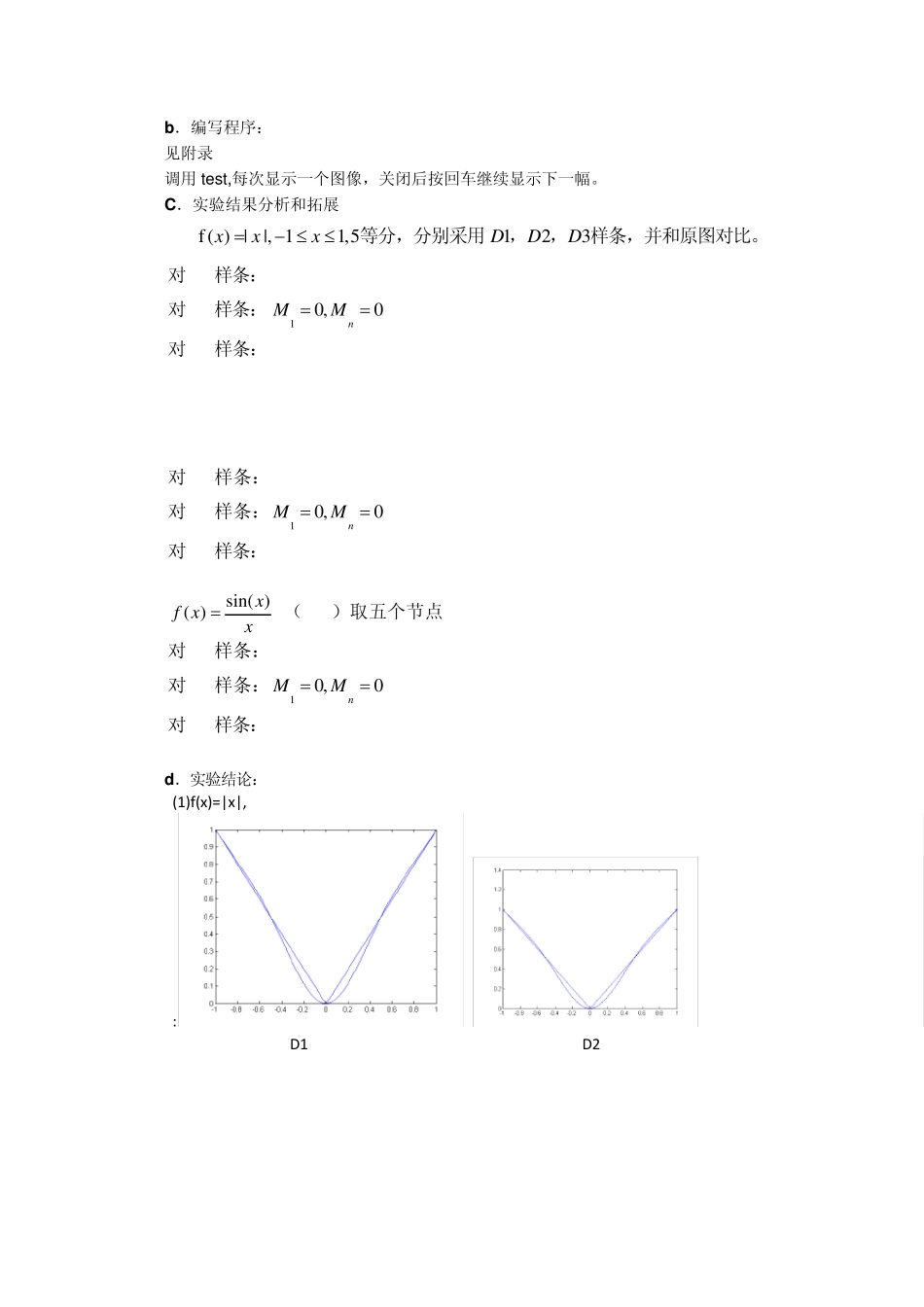
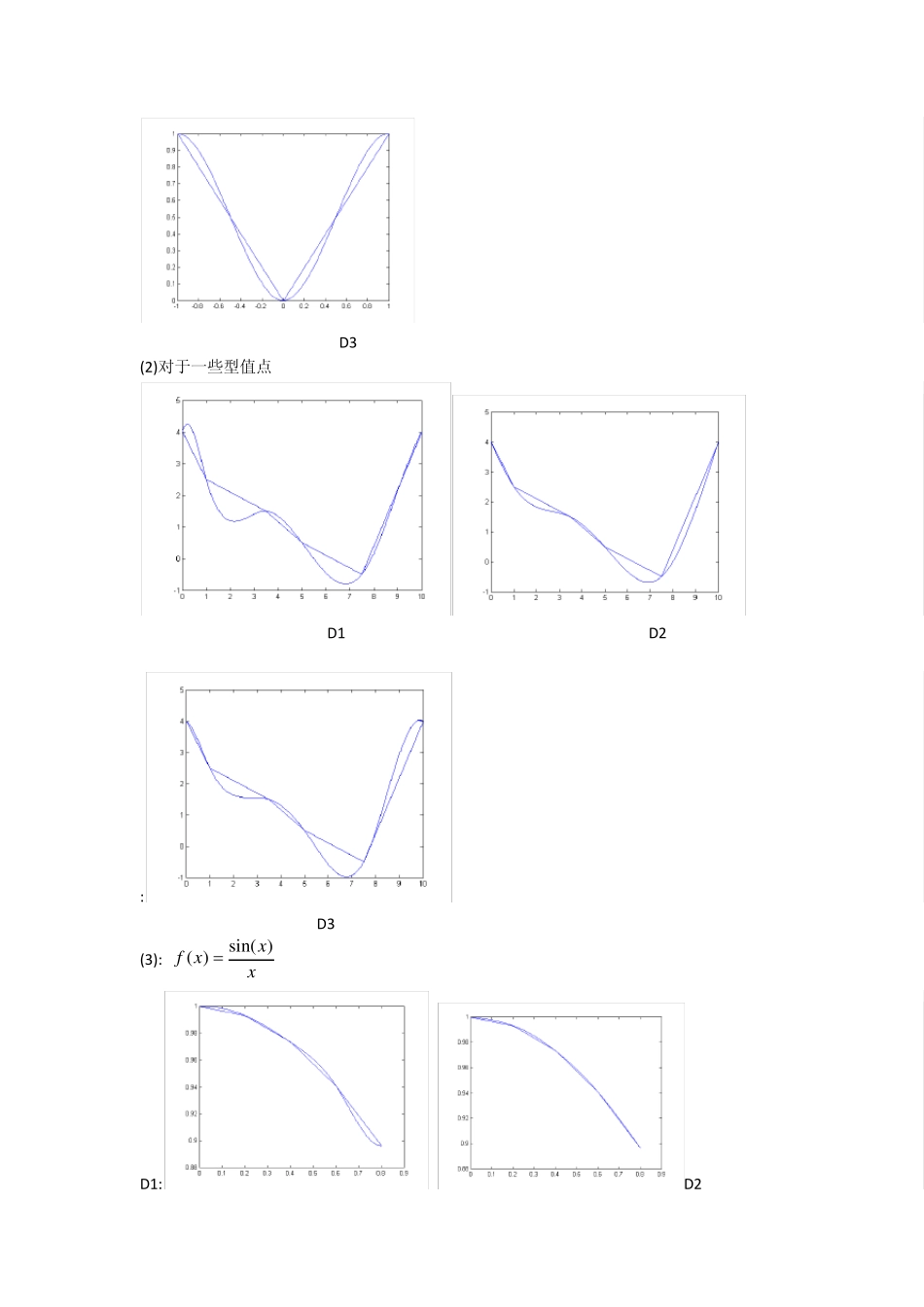
三次样条插值的数值实验 姓名: 王维滨 学号:0842011157 姓名: 李佳乐 学号:0842011034 姓名: 谢朝 学号:0842011062 姓名: 杨其荣 学号:0842011072 1.实验项目的性质和任务 对三次样条插值进一步理解,并编写matlab 程序,实现这些功能 2.算法设计和matlab 编程。 总前提: xi 第 i点的横坐标 iy 第 i点的纵坐标 iM ,,s 的记号 ,,,,,,23( )( )( )( )()()()2!3!iiiiiiisxsxs xys xxxxxxx 有数值逼近书上的推导,我们令: 111iiiiixxuxx, 111iiiiixxxx,11111111f(,,)iiiiiiiiiiiiiyyyyxxxxxx xxx 由于未知数的数目多于方程的个数,我们需要增加两个条件才能唯一确定一个分段三次函数 1)D1 的三次样条插值 a.实验方案与原理: 我们加上条件:,,,,11()(),()()nns xfxs xfx 我们建立三弯矩方程组: 1211211111126 ( ,,)26 (,,),2,3.....126 (,,)iiiiiiiinnnnnMMf x x xu MMMf xx xinMMf xx x 然后采用追赶法迭代求方程组,但是我们在程序中采用简单的方法(矩阵计算)直接求解降低编程难度, 2)D2三次样条插值 223123211i11112111126 ( ,,)26 (,,),3,4.....226 (,,)iiiiiiinnnnnnnnMMf x x xu Mu MMMf xx xinuMMf xx xM 3)D3三次样条插值 22321231i111211126 ( ,,)26 (,,),3,4.....126 (,,)niiiiiiinnnnnnnMMu Mf x x xu MMMf xx xinMu MMf xx x b.编写程序: 见附录 调用test,每次显示一个图像,关闭后按回车继续显示下一幅。 C.实验结果分析和拓展 (1)f( ) | |, 11,5123xxxDDD 等分,分别采用,,样条,并和原图对比。 对 D1样条:y11=-1,y1n=1 对 D2样条:10,0nMM 对 D3样条: (2) X=[0 1 3.5 5 7.5 10]; Y=[4 2.5 1.5 0.5 -0.5 4]; 对 D1样条:y11=2.5,y1n=1.4 对 D2样条:10,0nMM 对 D3样条: (3) sin( )( )xf xx,(0,1)取五个节点 对 D1样条:y11=0,y1n=0 对 D2样条:10,0nMM 对 D3样条: d.实验结论: (1)f(x)=|x|, : D1 D2 D 3 (2)对于一些型值点 D 1 D 2 : D 3 (3): sin( )( )xf xx D ...