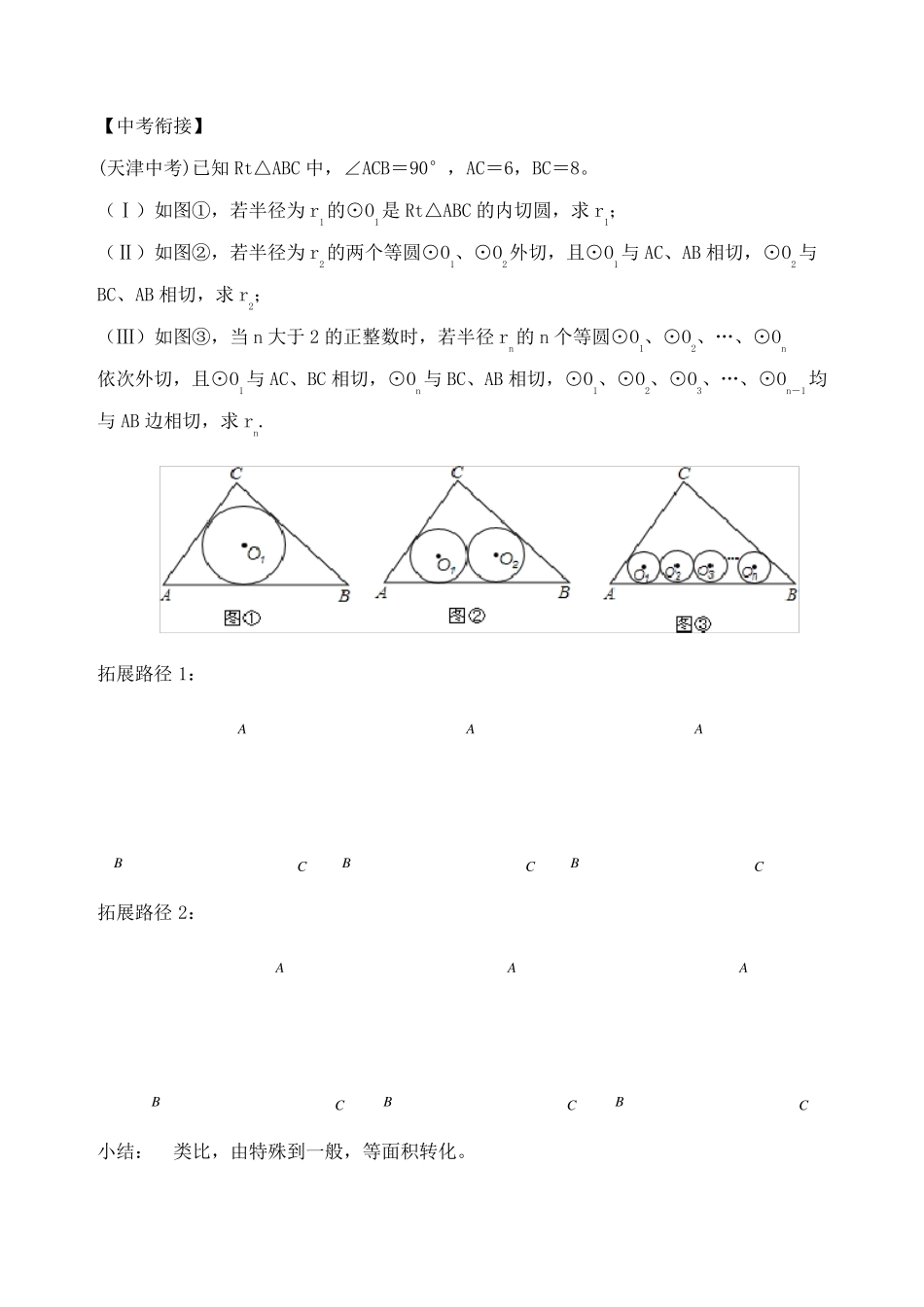
EFDOABC三角形的内切圆 ——与内切圆半径有关的计算 【学习目标】 1.理解三角形内切圆的有关概念。 2.掌握三角形的内心的位置、数量特征。 3.会求三角形的内切圆半径,会利用内心的相关性质解决计算问题。 【预备知识】 1.内切圆的有关概念 _________________________叫做三角形的内切圆,圆心叫做三角形的内心,三角形的内心是__________________________的交点。 2.内切圆的性质 (Ⅰ)内心的性质:_____________________________的距离相等。 (Ⅱ) 设 S 是△ABC 面积,a, b,c 是三角形三边长,r 为三角形内切圆半径,则三角形面积与其内切圆半径的关系为:S=______________ 特别地,直角三角形三边长与内切圆半径关系为: r=______________ 3. 切线长定理 经过圆外一点的切线,这一点和切点之间的线段长叫做这点到圆的切线长。从圆外一点引圆的两条切线,__________________,________________________________。 4.如何求一个三角形的面积 △ABC 中 a,b,c 是三角形的三边长,2abcp 方法① 海伦公式()()()Sp pa pb pc 方法② bcarrrDEFIBACCABD【中考衔接】 (天津中考)已知Rt△ABC 中,∠ACB=90°,AC=6,BC=8。 (Ⅰ)如图①,若半径为 r1的⊙O1是 Rt△ABC 的内切圆,求 r1; (Ⅱ)如图②,若半径为 r2的两个等圆⊙O1、⊙O2外切,且⊙O1与 AC、AB 相切,⊙O2与BC、AB 相切,求 r2; (Ⅲ)如图③,当 n 大于 2 的正整数时,若半径 rn的 n 个等圆⊙O1、⊙O2、…、⊙On 依次外切,且⊙O1与 AC、BC 相切,⊙On与 BC、AB 相切,⊙O1、⊙O2、⊙O3、…、⊙On-1均与 AB 边相切,求 rn. 拓展路径 1: CBACBACBA 拓展路径 2: CBACBACBA小结: 类比,由特殊到一般,等面积转化。 【实战演练】 【练习1】(2016 四川省攀枝花市)如图,△ABC 中,∠C=90°,AC=3,AB=5,D 为 BC边的中点,以 AD 上一点 O 为圆心的⊙O 和 AB、BC 均相切,则⊙O 的半径为 . 【练习2】(2011 年江苏省南通)如图,三个半圆依次相外切,它们的圆心都在 x 轴上,并与直线 y= 33 x 相切.设三个半圆的半径依次为 r1、r2、r3,则当 r1=1 时,r3= . 【练习3】(2016 年福建龙岩第 16 题)如图1~4,在直角边分别为 3 和 4 的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10 中有 10 个直角三角形的...