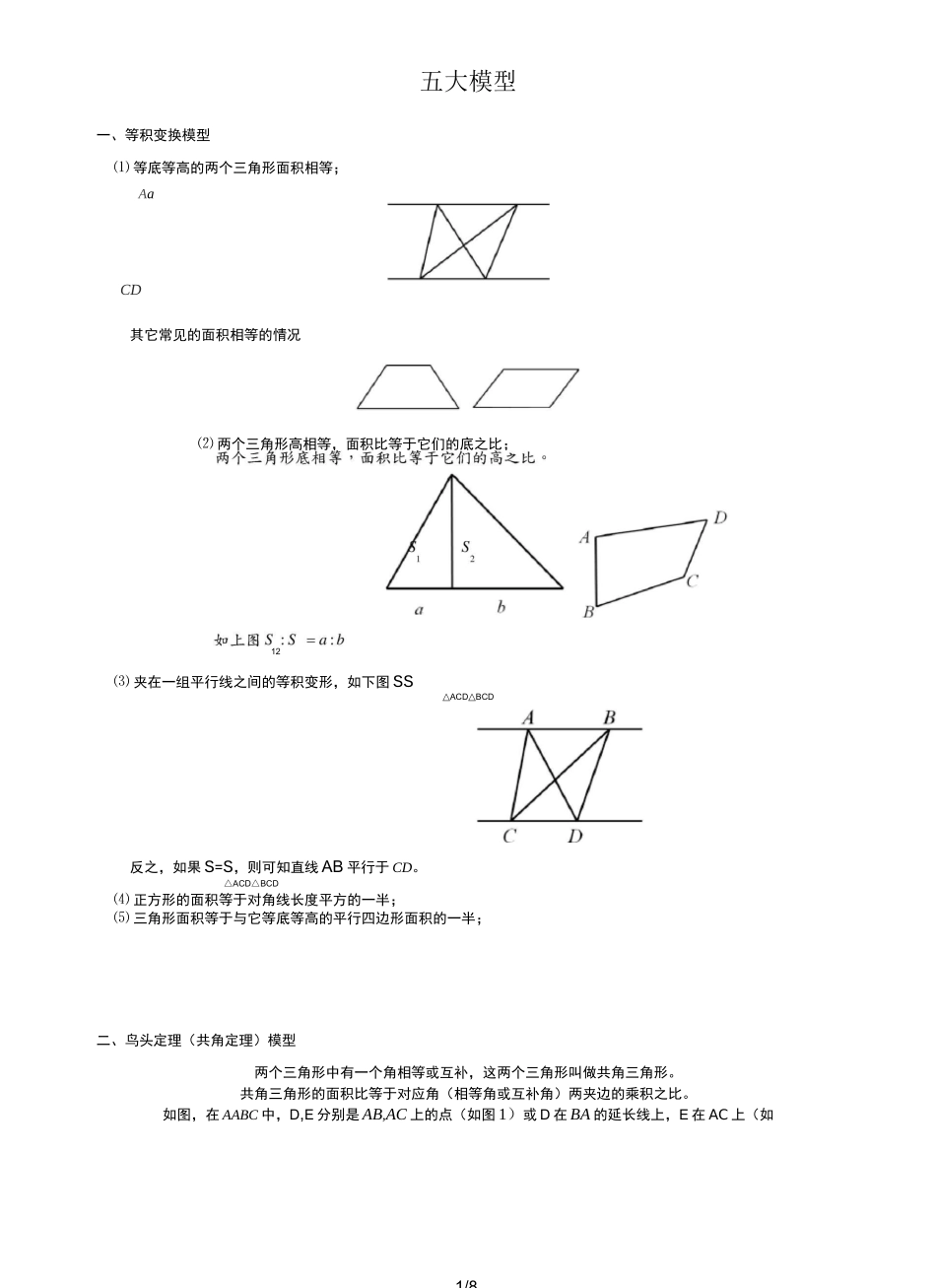
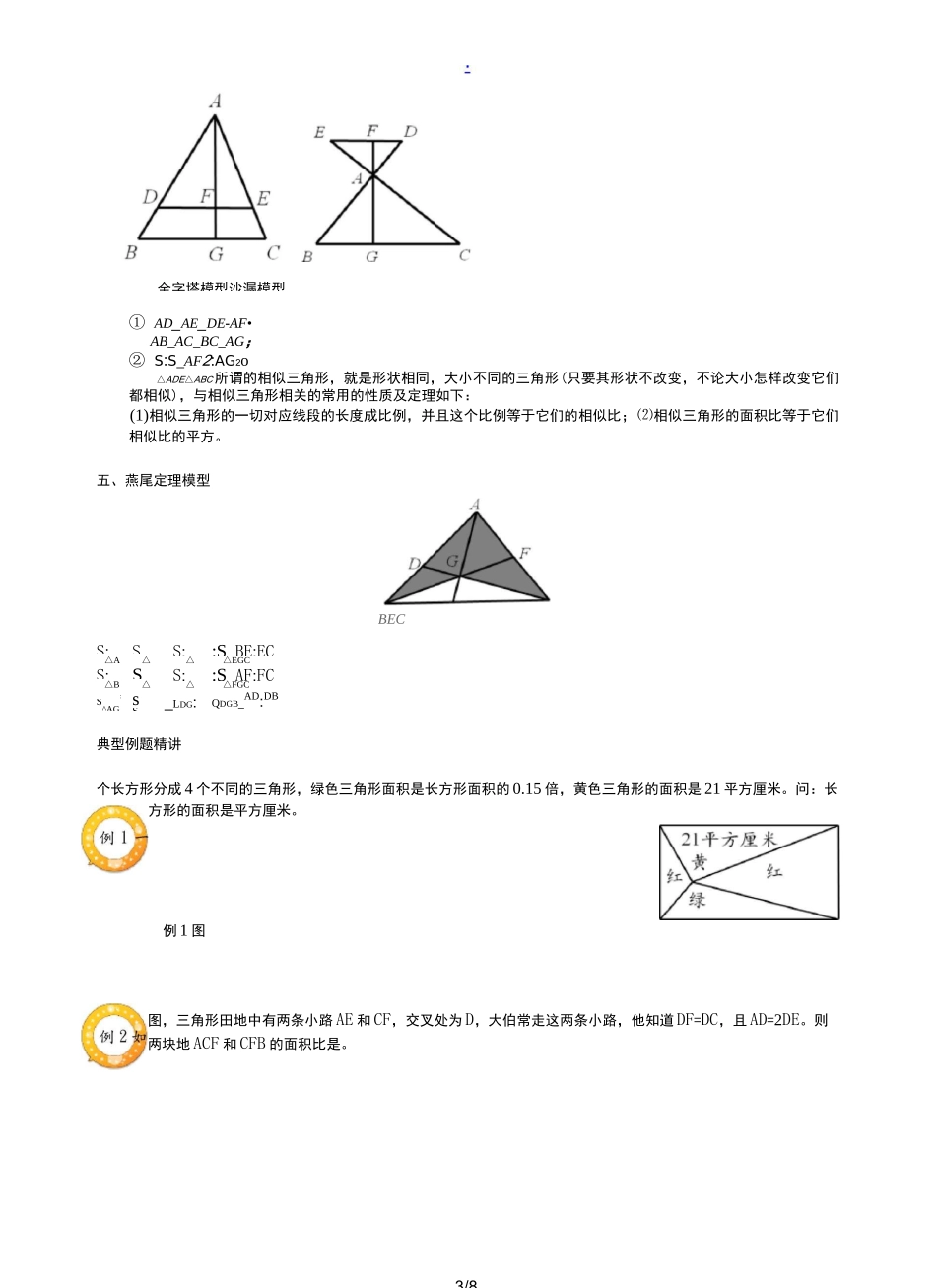
1/8五大模型一、等积变换模型⑴ 等底等高的两个三角形面积相等;AaCD其它常见的面积相等的情况⑵ 两个三角形高相等,面积比等于它们的底之比;12⑶ 夹在一组平行线之间的等积变形,如下图 SS△ACD△BCD反之,如果 S=S,则可知直线 AB 平行于 CD。△ACD△BCD⑷ 正方形的面积等于对角线长度平方的一半;⑸ 三角形面积等于与它等底等高的平行四边形面积的一半;二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。如图,在 AABC 中,D,E 分别是 AB,AC 上的点(如图 1)或 D 在 BA 的延长线上,E 在 AC 上(如2/8梯形中比例关系(“梯形蝴蝶定理”)DI图 2),则 S:S=(ABxAC):(ADxAE)△ABC△ADE图 1 图 2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①S:S=S:S 或者 SxS=SxS②AO:OC=(S+S):(S+S)124313241243蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。① S:S=a2:b213② S:S:S:S=a2:b2:ab:ab;1324③ 梯形 S 的对应份数为(a+b)2。四、相似模型相似三角形性质:3/8① AD_AE_DE-AF•AB_AC_BC_AG;② S:S_AF2:AG2o△ADE△ABC所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。五、燕尾定理模型S:S_S::S_BE:EC△A△△△EGCS:S_S::S_AF:FC△B△△△FGC:S^AG sS^B_LDG:QDGB_AD:DB典型例题精讲个长方形分成 4 个不同的三角形,绿色三角形面积是长方形面积的 0.15 倍,黄色三角形的面积是 21 平方厘米。问:长方形的面积是平方厘米。例 1 图图,三角形田地中有两条小路 AE 和 CF,交叉处为 D,大伯常走这两条小路,他知道 DF=DC,且 AD=2DE。则两块地 ACF 和 CFB 的面积比是。金字塔模型沙漏模型BEC14/8例 2 图举一反三】两条线段把三角形分为三个三角形和一个四边形,如图所示,三个三角形的面积分别是 3,7,7,则阴影四边形的面积是多少?举一反三图【拓展】如图,已知长方形 ADEF 的面积 16...