惯性矩的算法

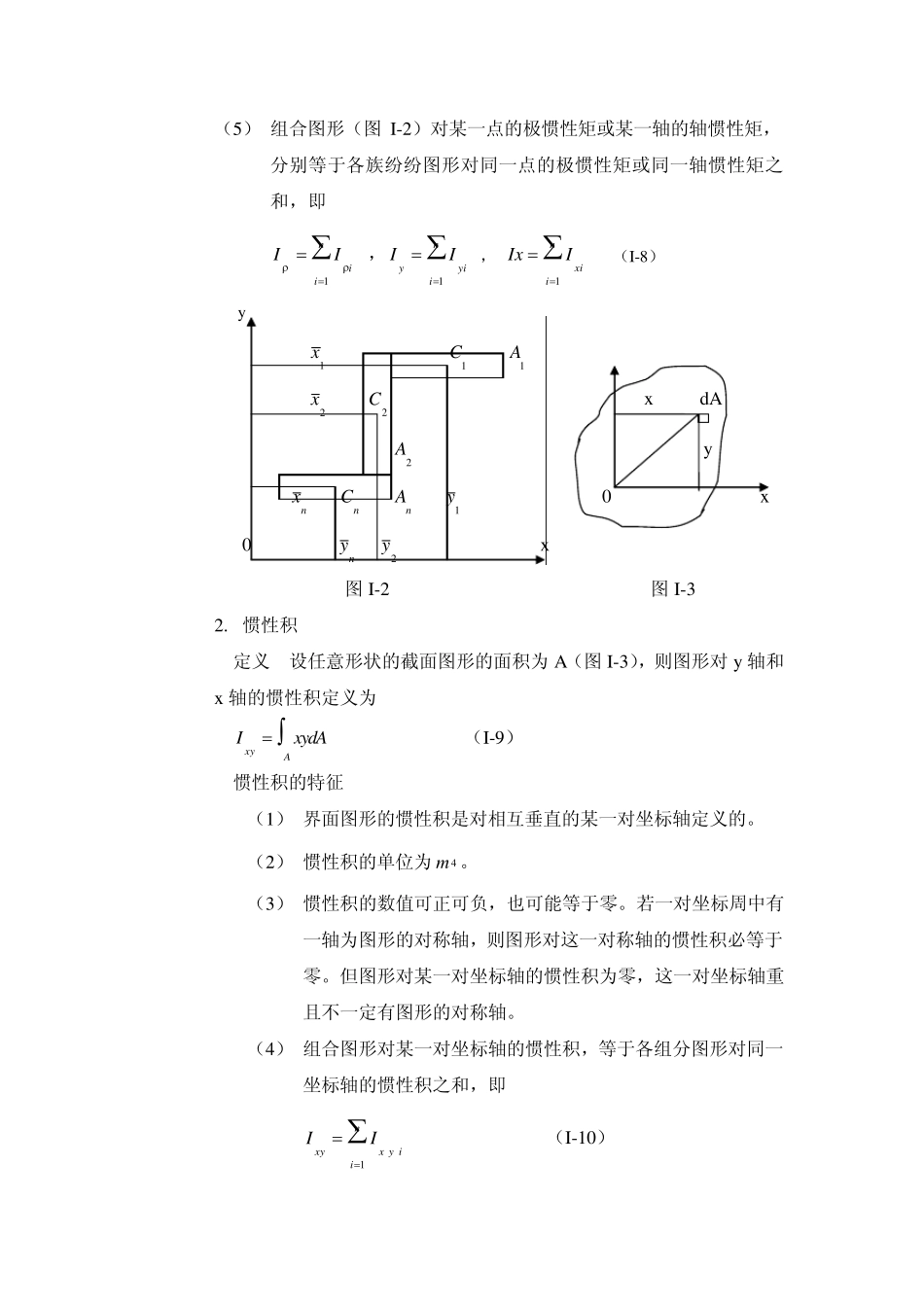
截面图形的几何性质 一.重点及难点： (一).截面静矩和形心 1.静矩的定义式 如图1 所示任意有限平面图形，取其单元如面积dA ，定义它对任意轴的一次矩为它对该轴的静矩，即 y ydAdSxxdAdSy x dA 整个图形对y、z 轴的静矩分别为 x ×C y AAyydASxxdAS （I-1） 0 A y x 2.形心与静矩关系 图I-1 设平面图形形心C 的坐标为CC zy , 则 0 ASyx ， ASxy （I-2） 推论 1 如果 y 轴通过形心（即0x），则静矩0yS；同理，如果 x 轴通过形心（即0y），则静矩0Sx；反之也成立。 推论 2 如果 x、y 轴均为图形的对称轴，则其交点即为图形形心；如果y 轴为图形对称轴，则图形形心必在此轴上。 3.组合图形的静矩和形心 设截面图形由几个面积分别为nAAAA321,,的简单图形组成，且一直各族图形的形心坐标分别为332211,,,yxyxyx；；，则图形对y 轴和x 轴的静矩分别为 niniiixixniiiniyiyyASSxAS1111S （I-3） 截面图形的形心坐标为 niiniiiAxAx11 ， niiniiiAyAy11 （I-4） 4.静矩的特征 (1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。 (2) 静矩有的单位为3m 。 (3) 静矩的数值可正可负，也可为零。图形对任意形心轴的静矩必定为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。 (4) 若已知图形的形心坐标。则可由式（I-1）求图形对坐标轴的静矩。若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。组合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静矩，然后由式（I-4）求出其形心坐标。 （二）.惯性矩 惯性积 惯性半径 1. 惯性矩 定义 设任意形状的截面图形的面积为A（图I-3），则图形对O 点的极惯性矩定义为 ApdAI2 （I-5） 图形对y轴和 x轴的光性矩分别定义为 AydAxI2 ， dAyIAx2 （I-6） 惯性矩的特征 （1） 界面图形的极惯性矩是对某一极点定义的；轴惯性矩是对某一坐标轴定义的。 （2） 极惯性矩和轴惯性矩的单位为4m 。 （3） 极惯性矩和轴惯性矩的数值均为恒为大于零的正值。 （4） 图形对某一点的极惯性矩的数值，恒等于图形对以该点为坐标原点的任意一对坐标轴的轴惯性矩之和，即 AxyApIIdAyxdAI)(222 （I-7） （5） 组合图形（图I-2）对某一点的极惯性矩或某一轴的轴惯性矩，分...