我写的讲义_应变理论

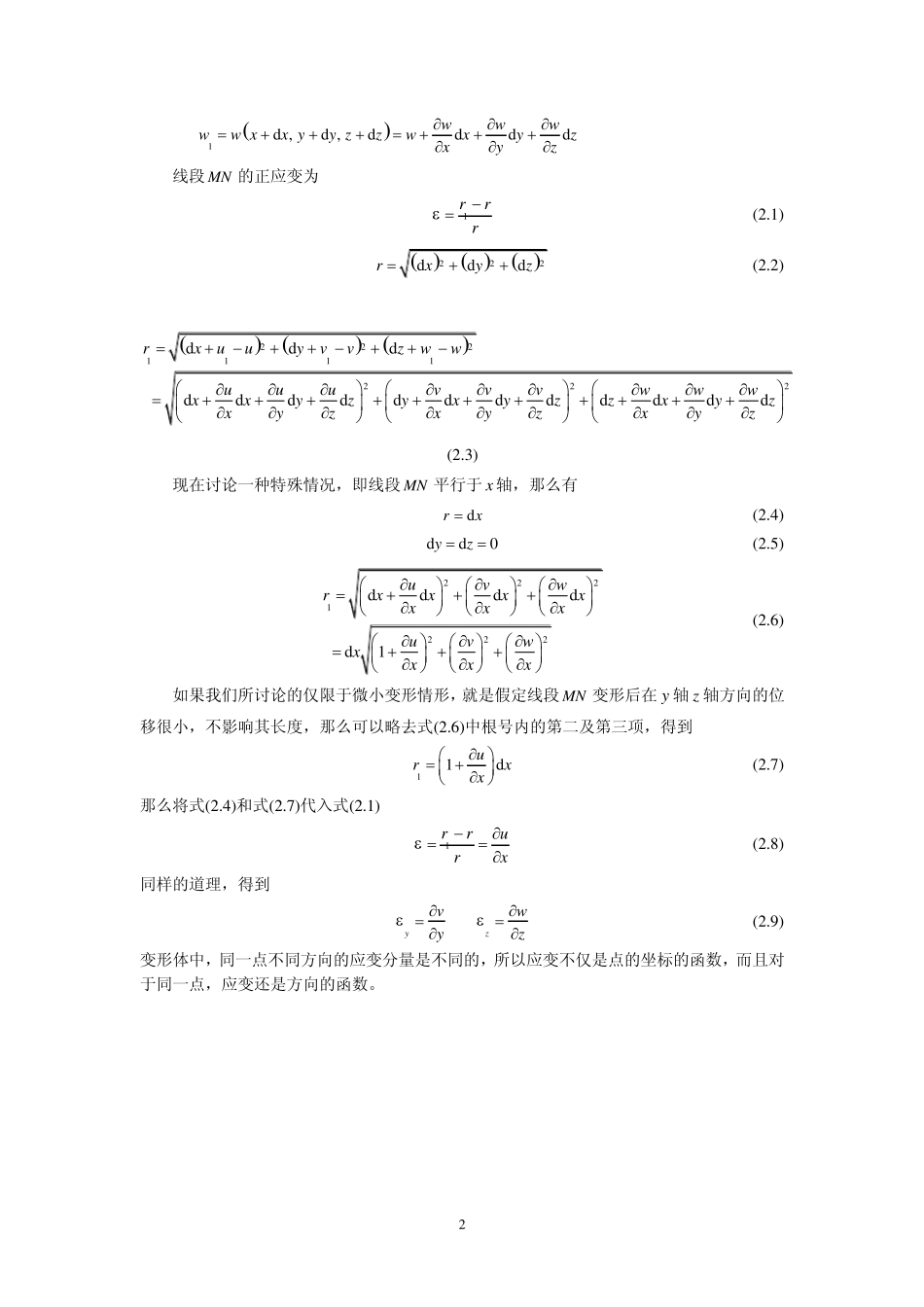
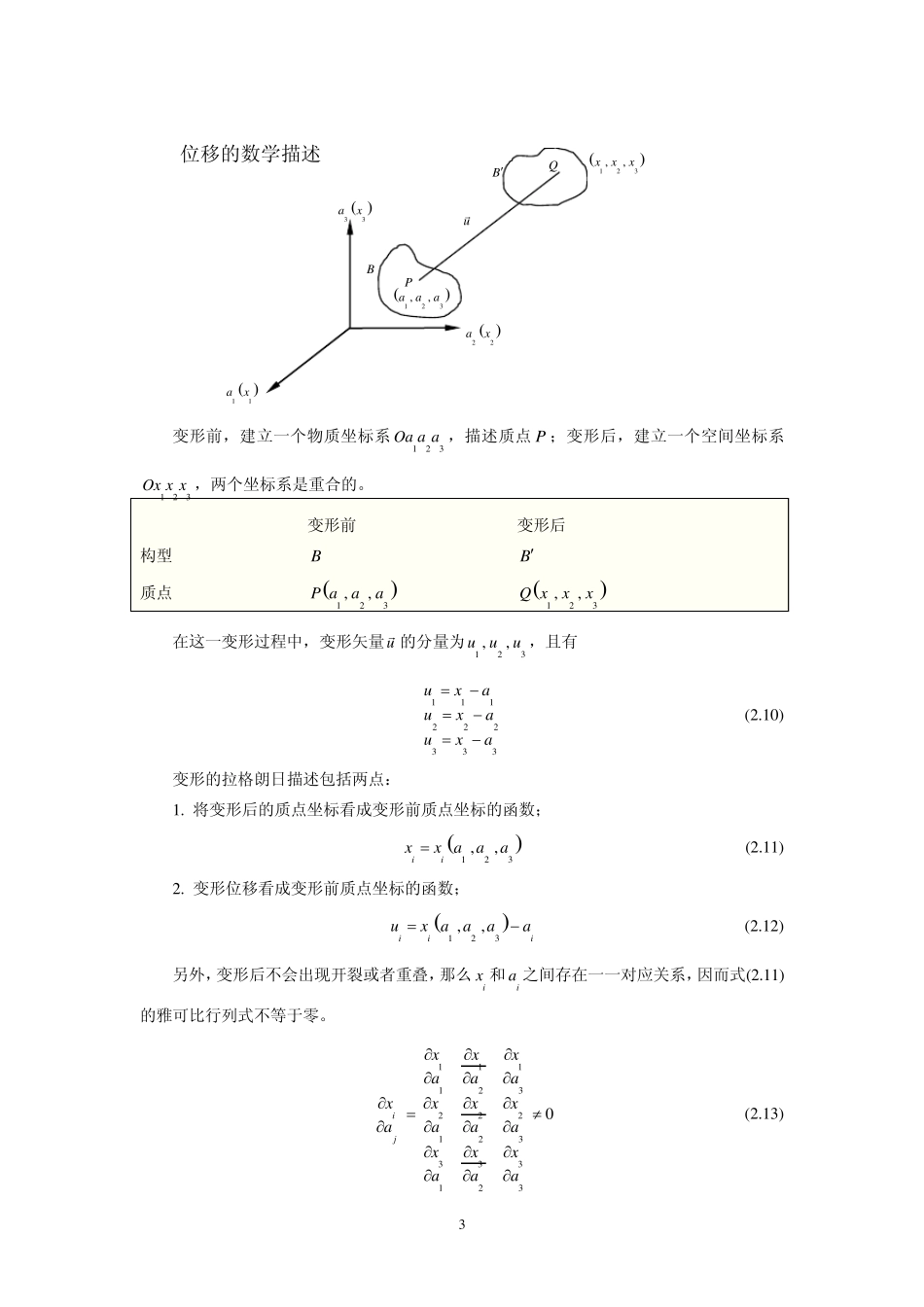
1 应变理论 参考文献： 1 王龙甫. 弹性理论. 科学出版社. 1 9 7 9 . 第2 章 2 陆明万, 罗学富. 弹性理论基础. 清华大学出版社. 1 9 9 0 . 第3 章 3 谢贻权. 弹性力学. 浙江大学出版社. 1 9 8 8 . 第4 章 4 黄怡筠, 程兆雄. 弹性理论基础. 北京理工大学出版社. 1 9 8 8 . 第3 章 5 朱滨. 弹性力学. 中国科技大学出版社. 2 0 0 8 . 第3 章 总体思路：进一步说明小变形应变方程；再定义格林应变；在小变形情况下，将格林应变简化成小变形应变。 3.1 对小变形应变的进一步说明(说明推导过程中的小变形假定) 变形前的坐标 变形量 变形后的坐标 , ,M x y z uvw 1,,Mxu yv zw d ,d ,dN xx yy zz 111uvw 1111d,d,dNxxuyyv zzw 其中， , ,uu x y z , ,vv x y z , ,ww x y z 1d ,d ,dddduuuuu xx yy zzuxyzxyz 1d ,d ,ddddvvvvv xx yy zzvxyzxyz yxz1111111d,d,dNxxyxzxd ,d ,dN xx yy zz1rr1111,,Mxyz,,M x y z 2 1d ,d ,ddddwwwww xx yy zzwxyzxyz 线段MN 的正应变为 1rrr (2 .1 )    222dddrxyz (2 .2 ) 2221111222dddddddddddddddrxuuyvvzwwuuuvvvwwwxxyzyxyzzxyzxyzxyzxyz (2 .3 ) 现在讨论一种特殊情况，即线段MN 平行于x 轴，那么有 drx (2 .4 ) dd0yz (2 .5 ) 2221222ddddd1uvwrxxxxxxxuvwxxxx (2 .6 ) 如果我们所讨论的仅限于微小变形情形，就是假定线段MN 变形后在y 轴z 轴方向的位移很小，不影响其长度，那么可以略去式(2 .6 )中根号内的第二及第三项，得到 11durxx (2 .7 ) 那么将式(2 .4 )和式(2 .7 )代入式(2 .1 ) 1rrurx  (2 .8 ) 同样的道理，得到 yzvwyz (2 .9 ) 变形体中，同一点不同方向的应变...