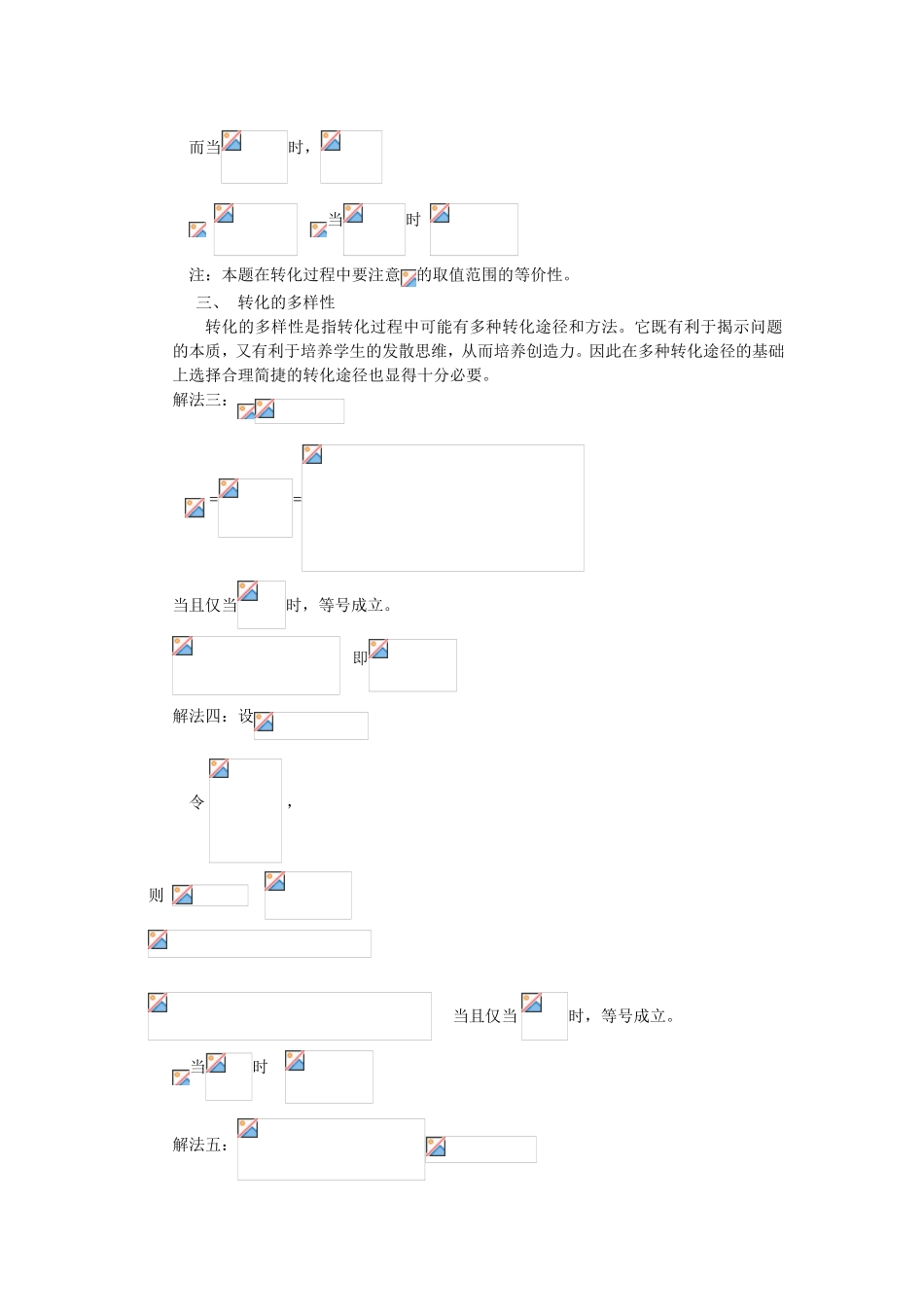
从一道题谈化归思想的培养数学思想方法是数学知识的精髓,数学教学中不仅是传授知识,更要注重学生的数学思想方法意识的培养,而各种数学思想方法都体现了化归的过程,因此化归思想无处不在。我们在化归过程中要能做到化难为易,化繁为简,化未知为已知。有这样一题:设求的最大值下面就结合本题的几种解法谈学生化归思想的培养中有几点应注意的问题。一、转化应具有有效性转化的有效性是指能使原问题化为简单熟知的问题。化归作为一种思想,它应包括转化的对象、目的、方法,因而在实施的过程中,应有明确的对象、设计目标、选择方法,其中设计目标为关键,而设计转化目标总是以已知的基本知识,基本方法在应用上已形成固定程序的问题为依据,使问题简单化,规范化。解法一:设直线则点到该直线的距离为而点P到直线的距离最大为OP=所以注:通过构造直线使所求问题转化为点到直线的距离,由这样数与形的转化,使问题简单化。二、转化的等价性转化的等价性是指转化前后满足充要条件,它是确保准确,顺利解决问题的前提条件。由于学生对转化的依据认识不清,在转化的过程中所出现的逻辑错误十分普遍,这是必须引起我们的高度注意。解法二:令,则由得而当时,当时注:本题在转化过程中要注意的取值范围的等价性。三、转化的多样性转化的多样性是指转化过程中可能有多种转化途径和方法。它既有利于揭示问题的本质,又有利于培养学生的发散思维,从而培养创造力。因此在多种转化途径的基础上选择合理简捷的转化途径也显得十分必要。解法三:==当且仅当时,等号成立。即解法四:设令,则当且仅当时,等号成立。当时解法五:令即解法六:把看着为特殊的常量的关于为变量的函数,这样也不失为一种方法。解法如下:设函数则求导数得:当时,函数为增函数;当时,函数为减函数。则当时,函数有最大值为。即注:本题比较深刻地考察了等价转换与化归的数学思想,本题的解答灵活地运用相关的知识技能,同时能否将原问题等价转化为自己所熟知的问题加以解决也是关键,也要有良好的观察力和一定深度的思维能力。