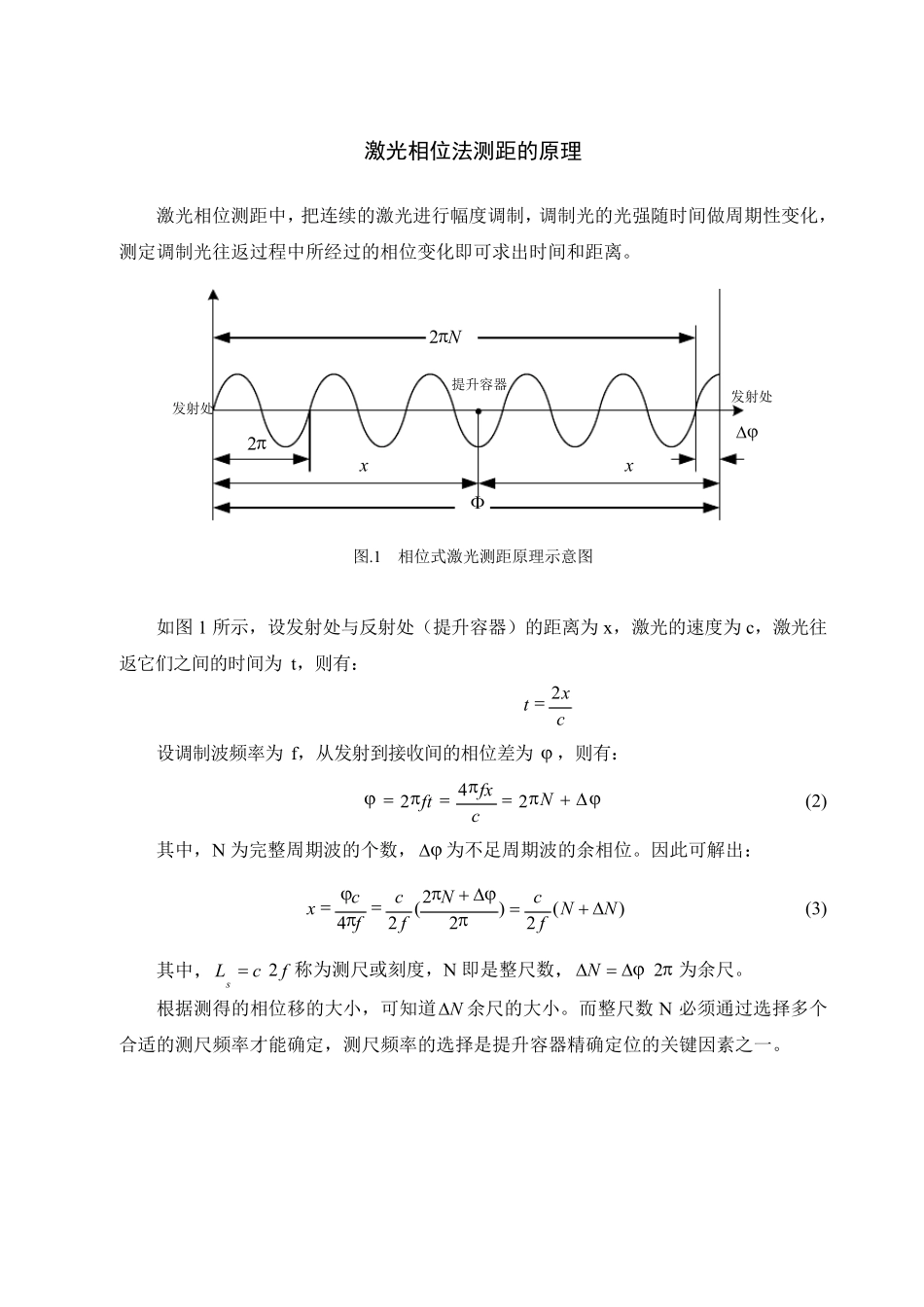
激光相位法测距的原理 激光相位测距中,把连续的激光进行幅度调制,调制光的光强随时间做周期性变化,测定调制光往返过程中所经过的相位变化即可求出时间和距离。 图.1 相位式激光测距原理示意图 如图 1 所示,设发射处与反射处(提升容器)的距离为 x ,激光的速度为 c,激光往返它们之间的时间为 t,则有: cxt2 设调制波频率为 f,从发射到接收间的相位差为 ,则有: Ncfxft242 (2) 其中,N 为完整周期波的个数,为不足周期波的余相位。因此可解出: )(2)22(24NNfcNfcfcx (3) 其中,fcLs2称为测尺或刻度,N 即是整尺数, 2N为余尺。 根据测得的相位移的大小,可知道 N余尺的大小。而整尺数 N 必须通过选择多个合适的测尺频率才能确定,测尺频率的选择是提升容器精确定位的关键因素之一。 2xxN2发射处 提升容器 发射处 多尺测量方法 测量正弦信号相移的方法都无法确定相位的整周期数,即不能确定出相位变化中 2的整倍数 N,而只能测量不足 2的相位尾数 ,因此公式(2.3)中的 N 值无法确定,使该式产生多个解,距离 D 就不能确定。解决此缺陷的办法是选用一个较低的测尺频率sf ,使其测尺长度sL 稍大于该被测距离,这种状况下不会出现距离的多值解。但是由于测相系统的测相误差,会导致测距误差,并且选用的sL 越大则测距误差越大。因此为了得到较高的测距精度而使用较短的测尺长度,即较大的测尺频率sf ,系统的单值测定距离就相应变小。 为了解决长测程和高精度之间的矛盾,一般使用的解决办法是:当待测距离 D 大于基本测尺sbL (精测测尺)时,可再使用一个或几个辅助测尺slL (又叫粗测测尺),然后将各个测尺测得的距离值组合起来得到单一的和精确的距离信息。由此可见,用一组测尺共同对距离 D 进行测量就可以解决距离的多值解,即用短尺保证精度,用长尺保证量程。这样就解决高精度和长测程的矛盾 [4]。 本系统选用 10 米作为精尺,1000 米作为粗尺,带入公式即可求得精尺频率和粗尺频率: 精尺频率 MHzLcf152510 (4) 粗尺频率 kHzLcf150210001000 (5) 其中,光速smc/1038。 上面公式计算出的只是个大概的数值,实际上光速要小于sm/1038,而且 c 还和实际的大气条件(比如矿井温湿度、气体成分、风速等)有关,因此,这些测尺频率需要进一步调整,具体...