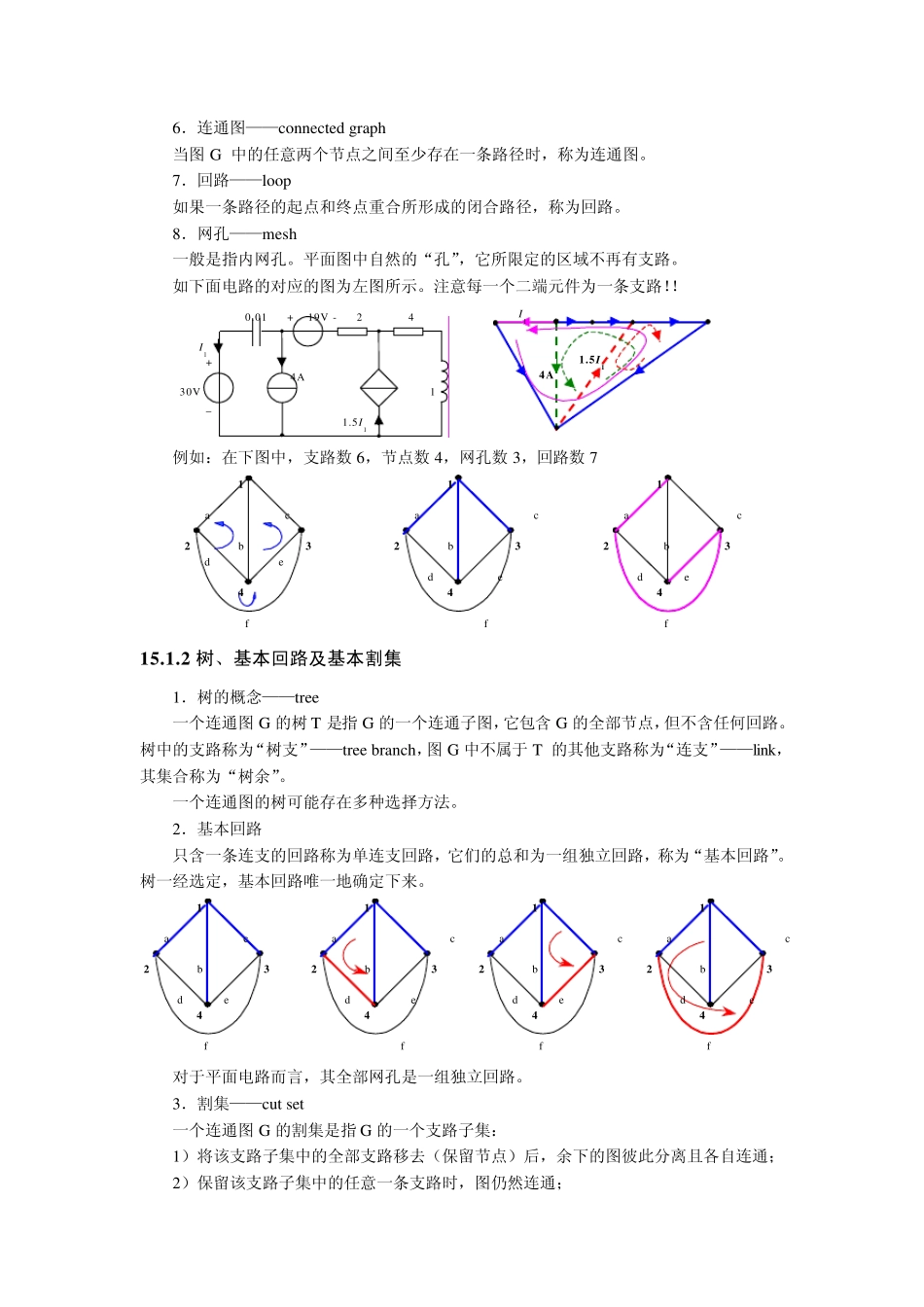
第十五章 电路方程的矩阵形式 重点: 1 . 关联矩阵、基本回路矩阵及基本割集矩阵等基本概念 2 . 熟练掌握几种基本矩阵的列写及其相互间关系 3 . 熟练掌握基于矩阵的大规模电路分析方法的原理及应用前景 难点: 1 . 掌握各种电路分析方法的矩阵应用 2 . 理解大规模电路分析方法对电路的计算机辅助分析与设计的作用 我们以前在学习支路电流法、支路电压法以及网孔分析法、节点分析法、割集分析法、回路分析法时,都是凭观察来列出所需的独立方程组。在求解方程时可以用手算,也可以使用电子计算机。对于含元件较少的电路,这种做法是行得通的。但是现代的电子电路可以包含数百个元件,特别是集成电路技术的飞越发展,电路日益复杂。对于这类“大规模(Large scale)电路”,不可能再凭观察来列写方程。需要有一种系统化的步骤来处理这类电路,使列写方程和求解的工作都能由电子计算机去完成。本章初步地介绍了这种分析方法。其中要用到上章所述图论的一些基本概念以及线性代数中的矩阵方法。 §1 5 -1 电网络图论的基本概念 网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。其中网络图论主要讨论电路分析中的拓扑规律性,从而便于电路方程的列写。 1 5 .1 .1 网络的图 1.网络图论——网络拓扑学 图论是数学中重要的分支,网络图论是图论在电路理论中的应用。主要通过电路的结构及其连接性质,对电路进行分析计算。 2.支路——Branch 每一个电路元件或多个电路元件的某种组合用一条线段代替,称为支路。 3.节点——node 每一个电路元件的端点,或多个电路元件相连接的点用一个圆点代替,称为节点。在电网络理论中,通常节点是指支路的汇集点,这一概念与数学图论中的“节点”概念略有不同。 4.网络的图——graph 节点和支路的集合,称为图,每一条支路的两端都连接到相应的节点上。有向图——Oriented graph 是指各个支路规定了参考方向的图反之,称为无向图。 5.路径——path 从图G 的某一节点出发,沿着一些支路连续移动,从而达到一个指定的节点,这一系列支路构成图的一条路径。 6.连通图——connected graph 当图G 中的任意两个节点之间至少存在一条路径时,称为连通图。 7.回路——loop 如果一条路径的起点和终点重合所形成的闭合路径,称为回路。 8.网孔——mesh 一般是指内网孔。平面图中自然的“孔”,它所限定的区域不再有支路。 如下面电路的对应的图为左...