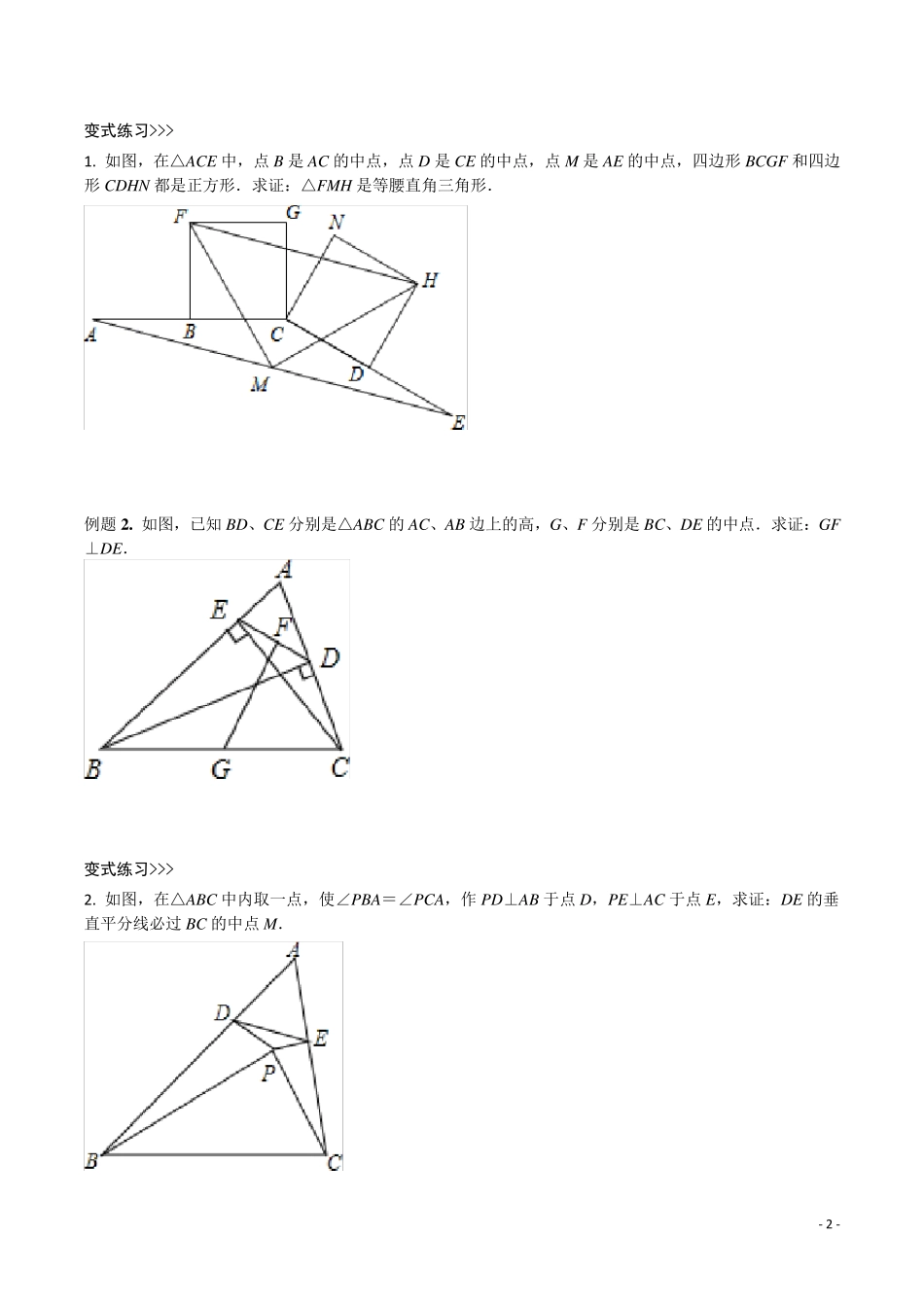
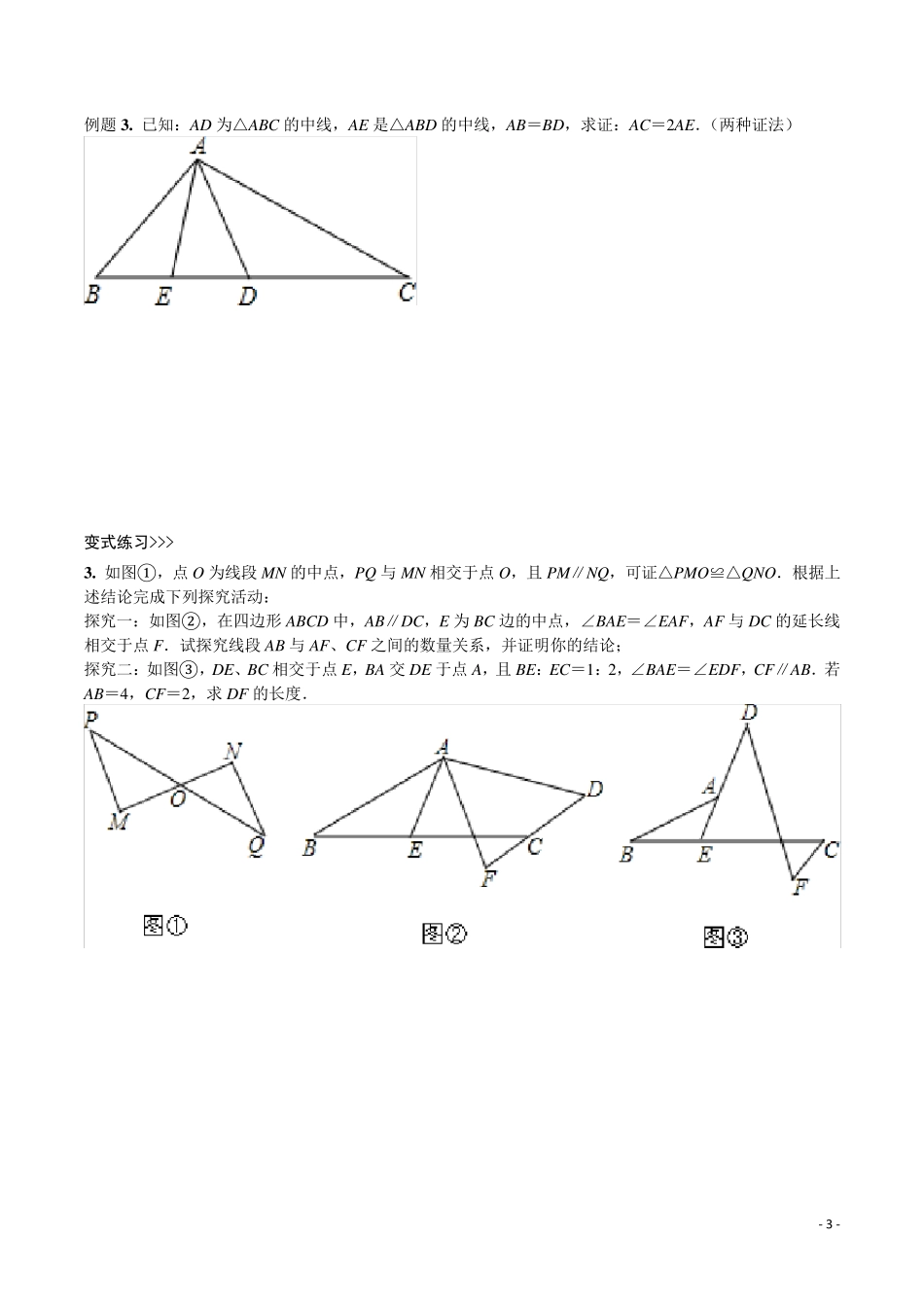
- 1 - 中考数学几何模型 4:中点模型 名师点睛 拨开云雾 开门见山 中点模型,提到中点,我们需要想到关于中点的以下知识点:①三角形中线平分三角形面积,等分点等分面积;②等腰三角形“三线合一”的性质;③直角三角形斜边上的中线等于斜边的一半;④三角形中位线平行且等于第三边的一半. 这四点使我们已经深入学习过的有关中点运用的知识点,今天重点在结合四点的基础上探究另外一种中点模型,我们简称“平中对模型”,即“平行线+中点+对顶角”构造全等或相似模型,与倍长中线法相通。 ABCDEABCDEFEDCBA 典题探究 启迪思维 探究重点 例题 1 . 如图,在△ABC 的两边 AB、AC 向形外作正方形 ABDE 和 ACFG,取 BE、BC、CG 的中点 M、Q、 N.求证:MQ=QN. - 2 - 变式练习>>> 1. 如图,在△ACE 中,点B 是AC 的中点,点D 是CE 的中点,点M 是AE 的中点,四边形BCGF 和四边 形CDHN 都是正方形.求证:△FMH 是等腰直角三角形. 例题 2 . 如图,已知BD、CE 分别是△ABC 的AC、AB 边上的高,G、F 分别是BC、DE 的中点.求证:GF ⊥DE. 变式练习>>> 2. 如图,在△ABC 中内取一点,使∠PBA=∠PCA,作 PD⊥AB 于点D,PE⊥AC 于点E,求证:DE 的垂 直平分线必过 BC 的中点M. - 3 - 例题 3 . 已知:AD 为△ABC 的中线,AE 是△ABD 的中线,AB=BD,求证:AC=2 AE.(两种证法) 变式练习>>> 3 . 如图①,点O 为线段MN 的中点,PQ 与MN 相交于点O,且PM∥NQ,可证△PMO≌△QNO.根据上 述结论完成下列探究活动: 探究一:如图②,在四边形ABCD 中,AB∥DC,E 为BC 边的中点,∠BAE=∠EAF,AF 与DC 的延长线相交于点F.试探究线段AB 与AF、CF 之间的数量关系,并证明你的结论; 探究二:如图③,DE、BC 相交于点E,BA 交DE 于点A,且BE:EC=1 :2 ,∠BAE=∠EDF,CF∥AB.若AB=4 ,CF=2 ,求DF 的长度. - 4 - 例题 4 . 如图,正方形ABCD 和正方形EFCG 的边长分别为3 和1 ,点F,G 分别在边BC,CD 上,P 为AE 的中点,连接PG,则PG 的长为 . 变式练习>>> 4 . 如图,过边长为3 的等边△ABC 的边AB 上一点P,作PE⊥AC 于 E,Q 为BC 延长线上一点,当 PA= CQ 时,连PQ 交 AC 边于 D,则DE 的长为 . - 5 - 例题5 . 如图1,在正方形ABCD 的边AB 上任取一点E,作EF⊥AB 交BD 于点F,取FD ...