胡汉才编著《理论力学》课后习题答案第3章习题解答

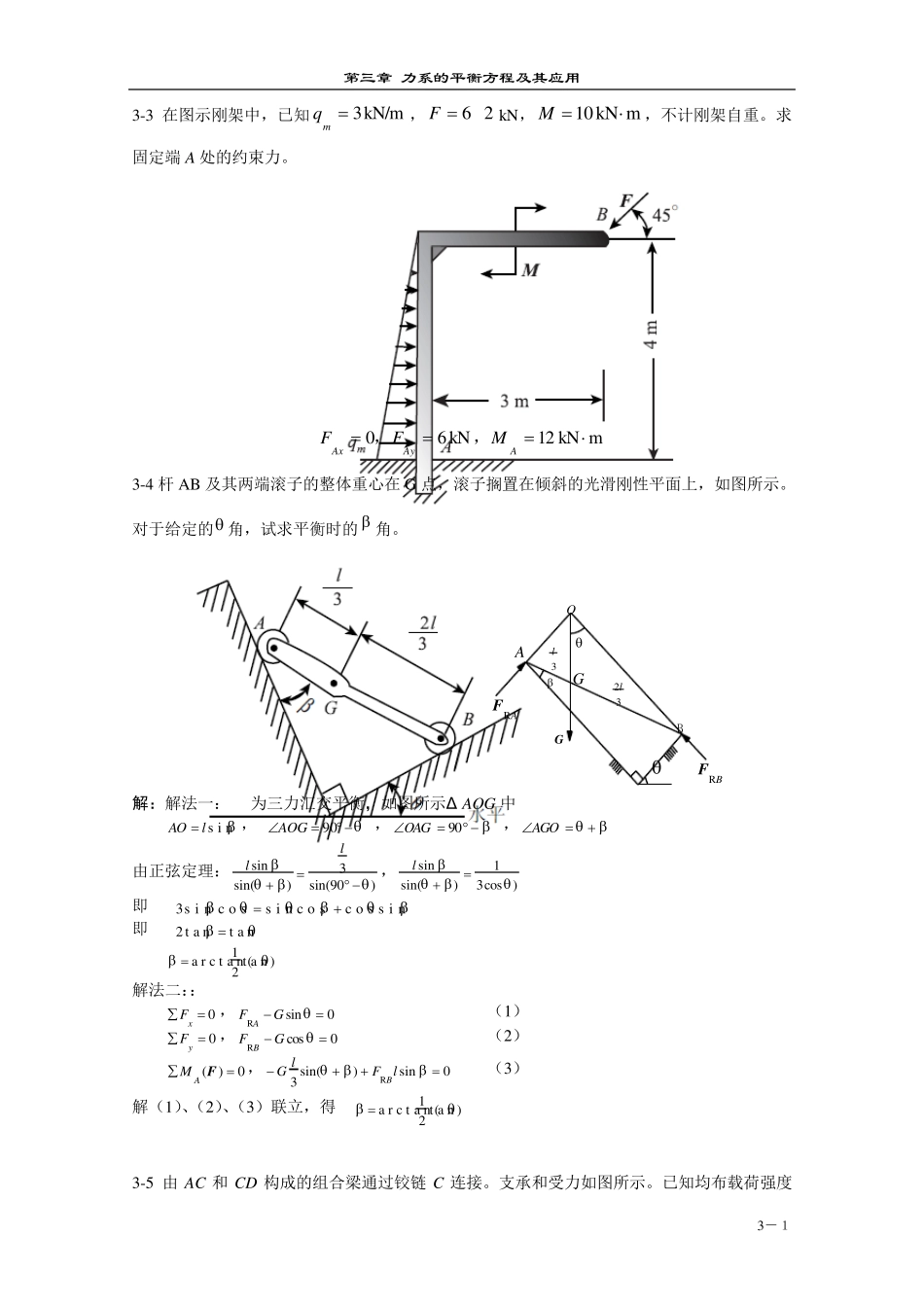
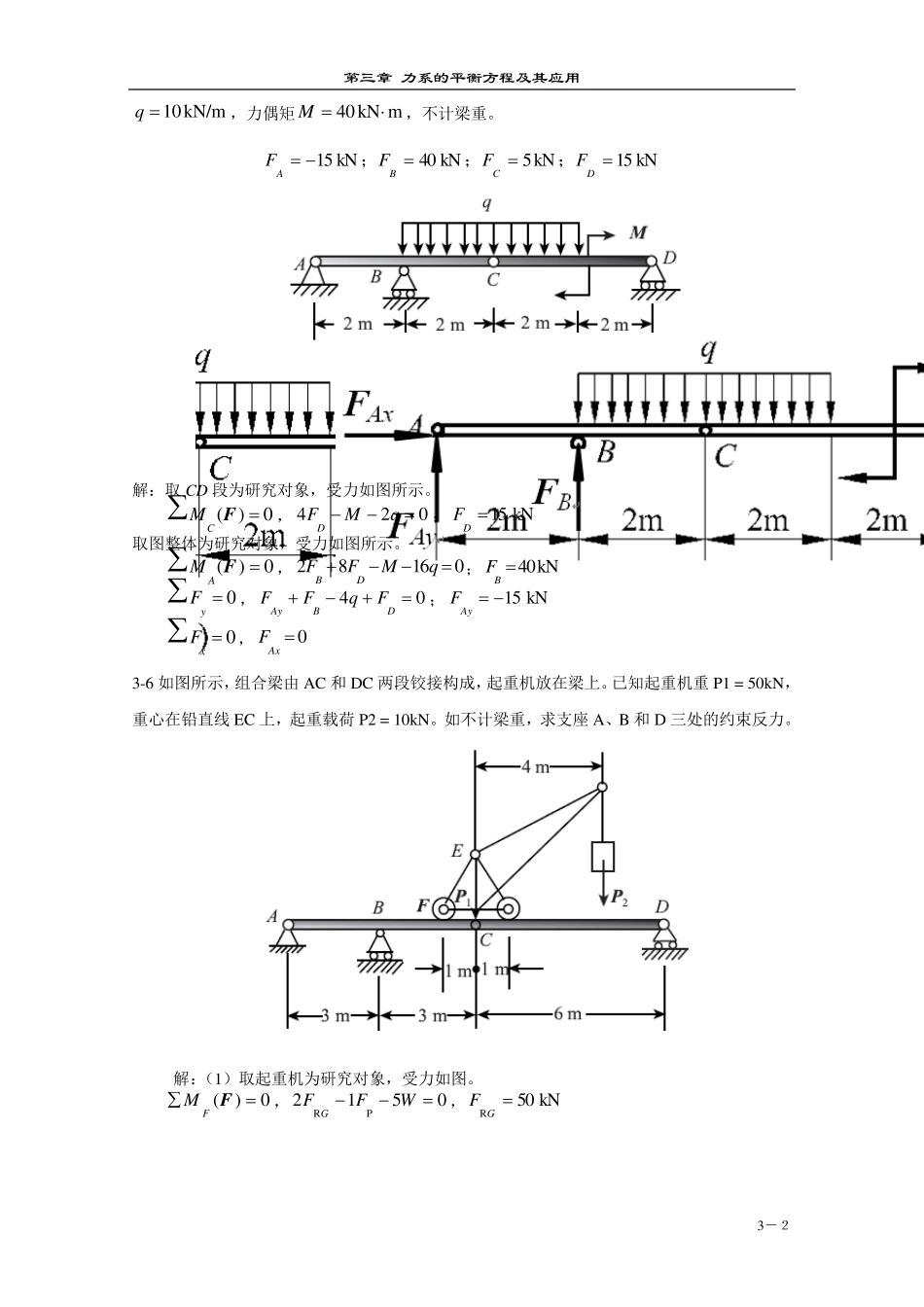
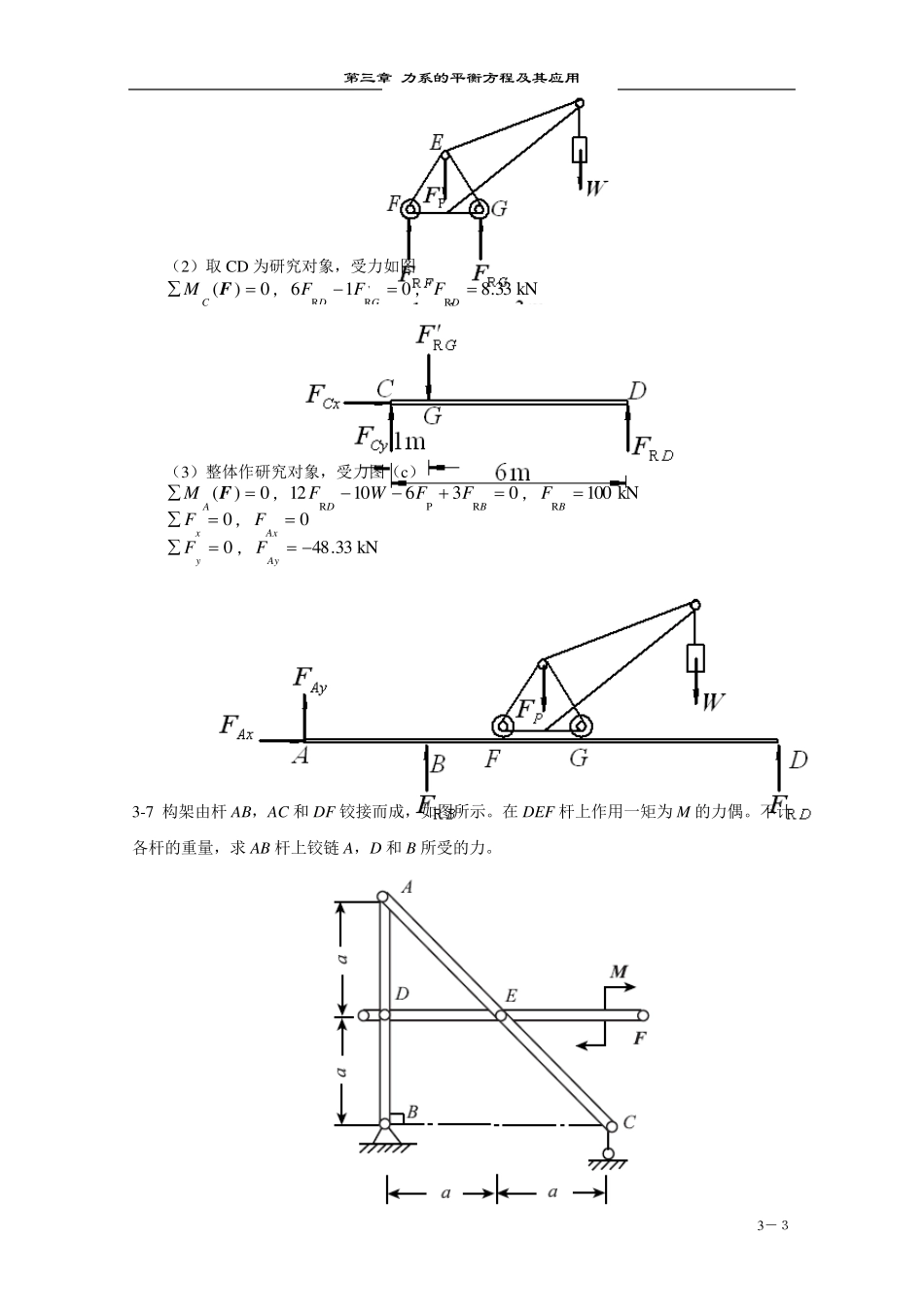
第三章 力系的平衡方程及其应用 3－１ 3-3 在图示刚架中，已知 kN/m3mq， 26FkN，mkN10M，不计刚架自重。求固定端A 处的约束力。 mkN12kN60AAyAxMFF，， 3-4 杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。对于给定的 角，试求平衡时的 角。 A3lGGBBRFARF32lO 解：解法一：AB为三力汇交平衡，如图所示Δ AOG 中 s i nlAO ， 90AOG ，90OAG ， AGO 由正弦定理：)90sin(3)sin(sinll，)cos31)sin(sinl 即 s i nc o sc o ss i nc o ss i n3 即 t a nt a n2 )t a n21a r c t a n (   解法二：： 0xF，0sinRGFA （1） 0yF，0cosRGFB （2） 0)(FAM，0sin)sin(3RlFlGB （3） 解（1）、（2）、（3）联立，得 )t a n21a r c t a n (   3-5 由AC 和 CD 构成的组合梁通过铰链 C 连接。支承和受力如图所示。已知均布载荷强度第三章 力系的平衡方程及其应用 3－２ kN/m10q，力偶矩mkN40M，不计梁重。 kN15kN5kN40kN15DCBAFFFF；；； 解：取CD 段为研究对象，受力如图所示。 0)(FCM，024qMFD；kN15DF 取图整体为研究对象，受力如图所示。 0)(FAM，01682qMFFDB； kN40BF 0yF，04DBAyFqFF；kN15AyF 0xF，0AxF 3-6 如图所示，组合梁由AC 和DC 两段铰接构成，起重机放在梁上。已知起重机重P1 = 50kN，重心在铅直线EC 上，起重载荷P2 = 10kN。如不计梁重，求支座A、B 和D 三处的约束反力。 解：（1）取起重机为研究对象，受力如图。 0)(FFM，0512PRWFFG，kN 50RGF 第三章 力系的平衡方程及其应用 3－３ （2）取CD 为研究对象，受力如图 0)(FCM，016'RRGDFF，kN 33.8RDF （3）整体作研究对象，受力图（c） 0)(FAM，0361012RPRBDFFWF，kN 100R BF 0xF，0AxF 0yF，kN 33.48AyF 3-7 构架由杆AB，AC 和DF 铰接而成，如图所示。在 DEF 杆上作用一矩为M 的力偶。不计各杆的重量，求 AB 杆上铰链 A，D 和B 所受的力。 第三章 力系的平衡方程及其应用 3－４ 3-8 图示构架中，物体P 重1200N ，由...