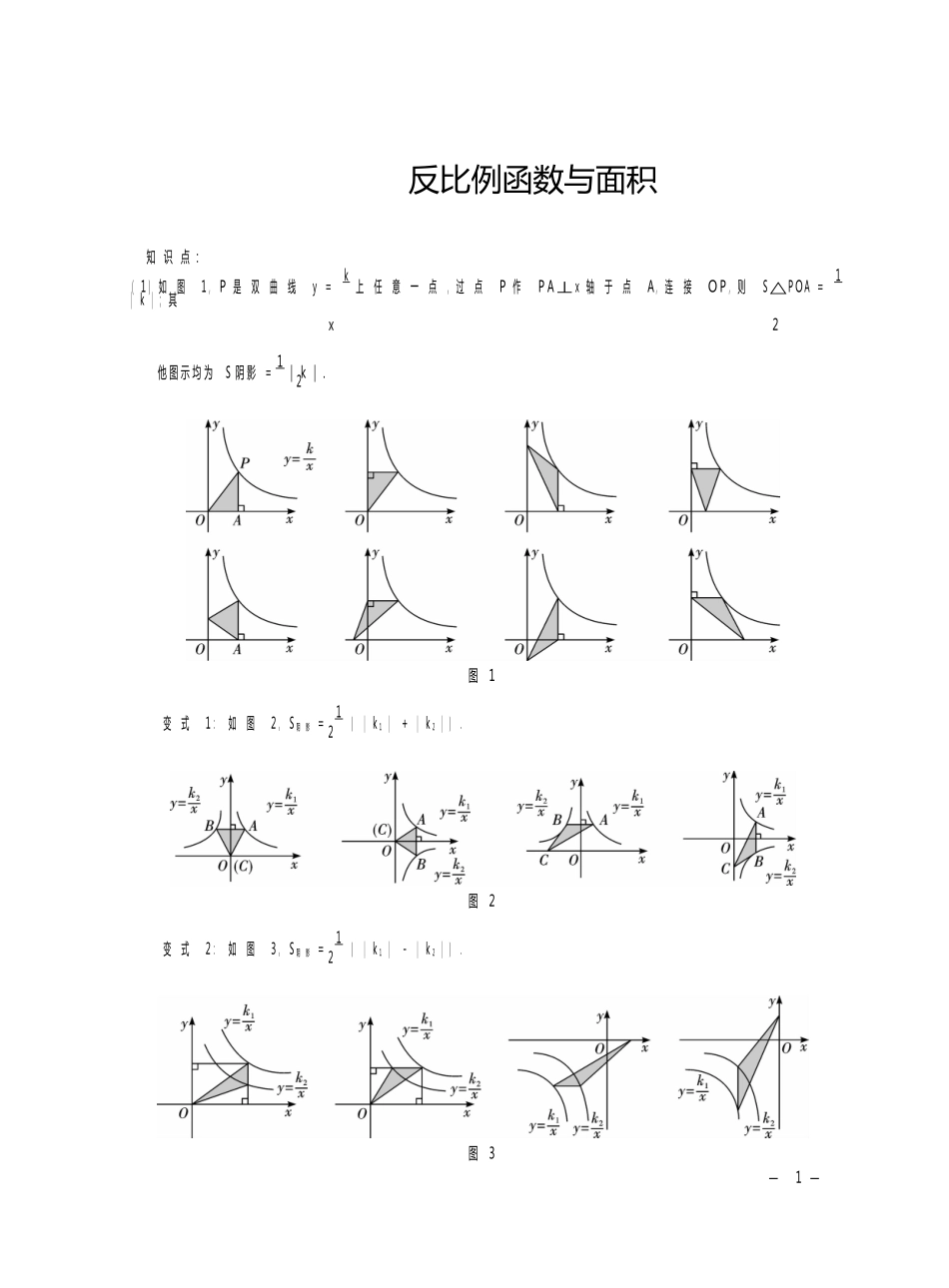
222反比例函数与面积 知 识 点 :( 1) 如 图 1, P 是 双 曲 线 y = k 上 任 意 一 点 , 过 点 P 作 PA⊥x 轴 于 点 A, 连 接 OP, 则 S△POA = 1 | k | ; 其x2 他 图 示 均 为S 阴 影 =1 | k | . 图 1变 式 1: 如 图 2, S阴 影 = 1 ( | k1 | + | k2 | ) . 图 2变 式 2: 如 图 3, S阴 影 = 1 ( | k1 | - | k2 | ) . 图 3— 1 —xxx( 2) 如 图 4, P 是 双 曲 线 y = k 上 任 意 一 点 , 过 点 P 作 PA⊥x 轴 于 点 A, PB⊥y 轴 于 点 B, 则 S矩 形 PAOB = | k | ; 其 他 图 示 均 为S 阴 影 = | k | . 图 4变 式 : 如 图 5, S阴 影 = | k1 | + | k2 | . 图 5( 3) 如 图 6, 过 原 点 O 作 直 线 交 双 曲 线 y = k 于 点 P, Q, 分 别 过 点 P, Q 作 y 轴 , x 轴 的 平 行 线 , 交 于 点A, 则 S△PAQ = 2 | k | ; 其 他 图 示 均 为 S阴 影 = 2 | k | . 图 6( 4) 如 图 7, 已 知 A, B 是 双 曲 线 y = k 同 一 支 上 的 两 点 , 分 别 过 点 A, B 作 AC⊥x 轴 ( 或 y 轴 ) 于 点 C,BD⊥x 轴 ( 或 y 轴 ) 于 点 D, 连 接 OA, OB, 则 S△AOB = S四 边 形 ABDC. 图 7— 2 —xxxxxx1. 如 图 , 已 知 A, B 是 双 曲 线 y = k ( k > 0 ) 第 一 象 限 上 的 两 点 , 连 接 OA, OB, 过 点 A 作 AM⊥x 轴 于 点M, 交 OB 于 点 C, 过 点 B 作 BN⊥x 轴 于 点 N, 则 SAOC与 S四 边 形 BCMN的 大 小 关 系 是 . 第1 题 图 第2 题 图 第3 题 图2. 如 图 , A 是 反 比 例 函 数 y = 2 - 槡2 ( x > 0) 的 图 象 上 任 意 一 点 , AB⊥y 轴 于 点 B, C 是 x 轴 上 的 动 点 , 则△A...