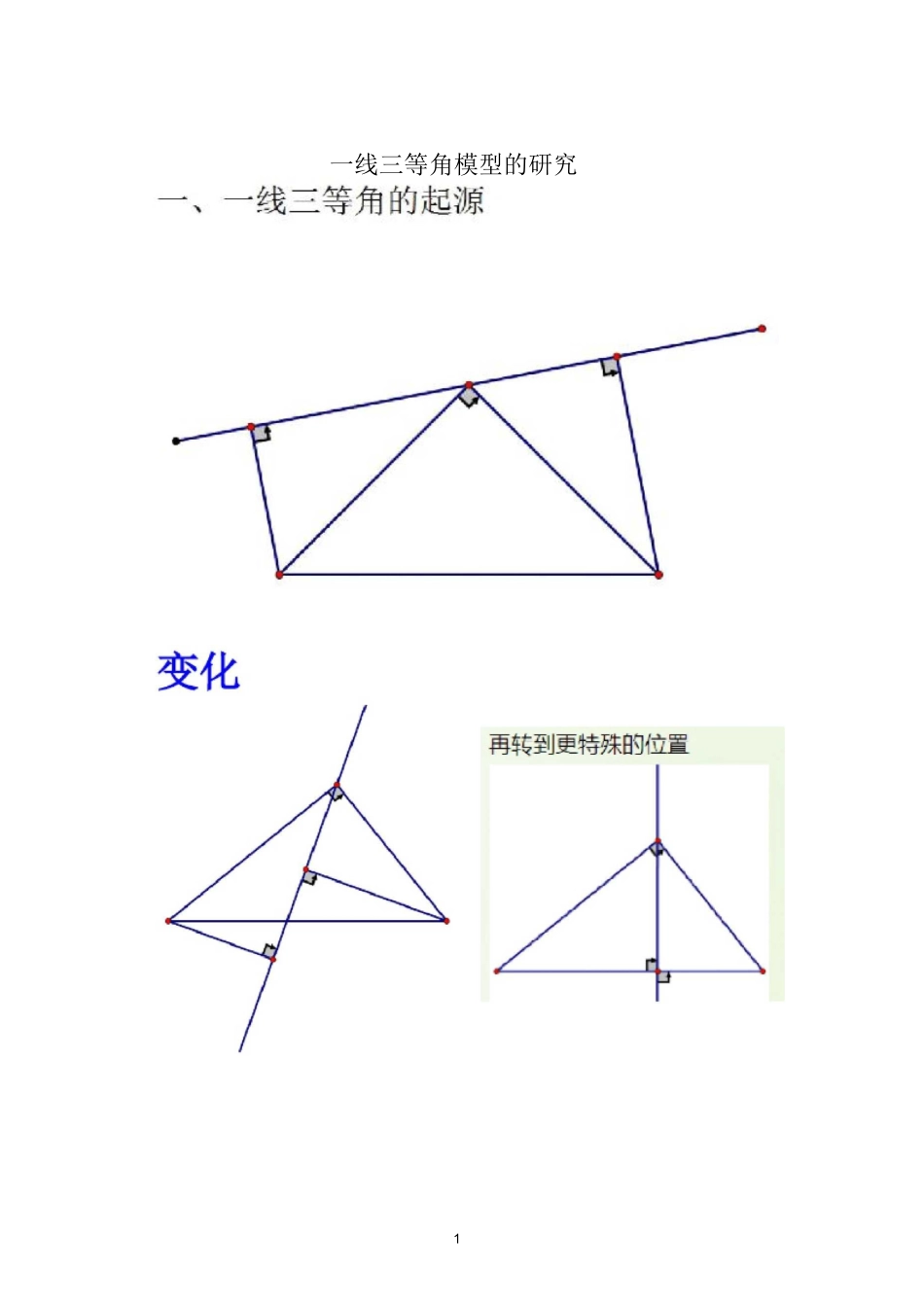
1一线三等角模型的研究EBA2D2.二等角分居直线的两侧2D2£B”一线三等角"有如下两种基 4 类型1.三等角都在直线的同侧D£AB2、当等角所对的边相等时的两个三角形全等.如图,当 CE-ED 时,易得△AEC=ABDE.D23AEB二、纵一线三等角的性质1、一般情况,由 Z1=Z2=Z3 易得△AISCs/VBDE3EN2BD*加画两条垂线一线三等角又和四边形中的半角模型联系在一起了A半角模型:EF-EMIFN-所以说,中点这个位置有点特殊EF3BD3 齐^中点型一线三等角^的特殊性质如图,^Z1=Z2=Z3ftD 是 EC 中点时,ABDEs△CFDsADFE,4238DC•A 与 E 重合时如图所乐EBD-四、一线三等角的常见构图(以等腰三角形为例)O5B6E.F3D•也可以在射线上A23BE五、具体案例1■如图,B>E、C 在同一直线上,且 ZB-ZC-ZAED-900。你能得出哪些结论?如果 E 为 BC中点呢?EB2.常见类型7由于角顶点位置的改变,或角绕顶点旋转会产生各种各样的变式,但万变不离其宗:都是构造相似三角形列比例式解决问题.3*考题赏析(MM 安徽:血如風正方形粧⑴的四个顶点分别在四条平行绑"jG 山这口条直线中相邻两争之间的距离恆戈为%》Lh(\j^>0F>0)(1) 求证;”打 d⑵ 设正方形胡门的面税为矢采证:2 呜":+耐;⑶ 若訊-施=1 丿当破灿说明正方形 ABCL 的面积 5 随洞娈化情卅・松C,ZM=ZA=ZE=a’〔2009 安徽省)22.如團」为 g 髯殳描的中駄腿芍孔交于点匸 DM 交圧于*临交 BC 于臥匸⑴ 写出團中三疤相似三角形,并证明苴中的一对;dM891.[典“年宜宾、如冏*存也 AEC 中.F1■热 AB 二航二®BC=6,冃厶 AE-C^ADEF,将AEEFJ^AABC 重合在一起,Z\ABC 不动,ADEF 动,井满足=点卫在边號上沿 B 到 C 的方向压动,且 DE 始终经过点扎 EF 与 AC 交于 H 庶八(1)求证,AABEO^A5CJH;^〔肚探究;在 ADF3■远动过程中・垂畫部令能否构成等腰才雋形.若能.求出 BE 的长 m 若不能,请说明理由:屮(3)当线段 AM 最矩时,求重畳部分的面积。」2.:殳 011 詢北荆州)知耳 P 为线段 AB 上一点,AD 与眈交于 E・ZCPD=ZA-ZB(EC 交PD±F,屈交 PQ-HG,则图中殆似三堀形有"A.1D.2#C.3 对 D.4 对+■3.(女飙二湖如 1L 模拟)如罔,在等边△AEC 中,D;^EC 边上一点.EAC 边上一福:且 ZM)E=CO4,BDW,C3=2,则△ABC 的边长为(')*A.9B.12C.15D.边屮4•问题推广•推广 1;如图 1,已知四边形 ABCD 中,ZB=ZC,平分线乜AF.DE 分别是 ZBAD 与 ZCDA 的•结论:AABF<^AECDo1判申命题"平...