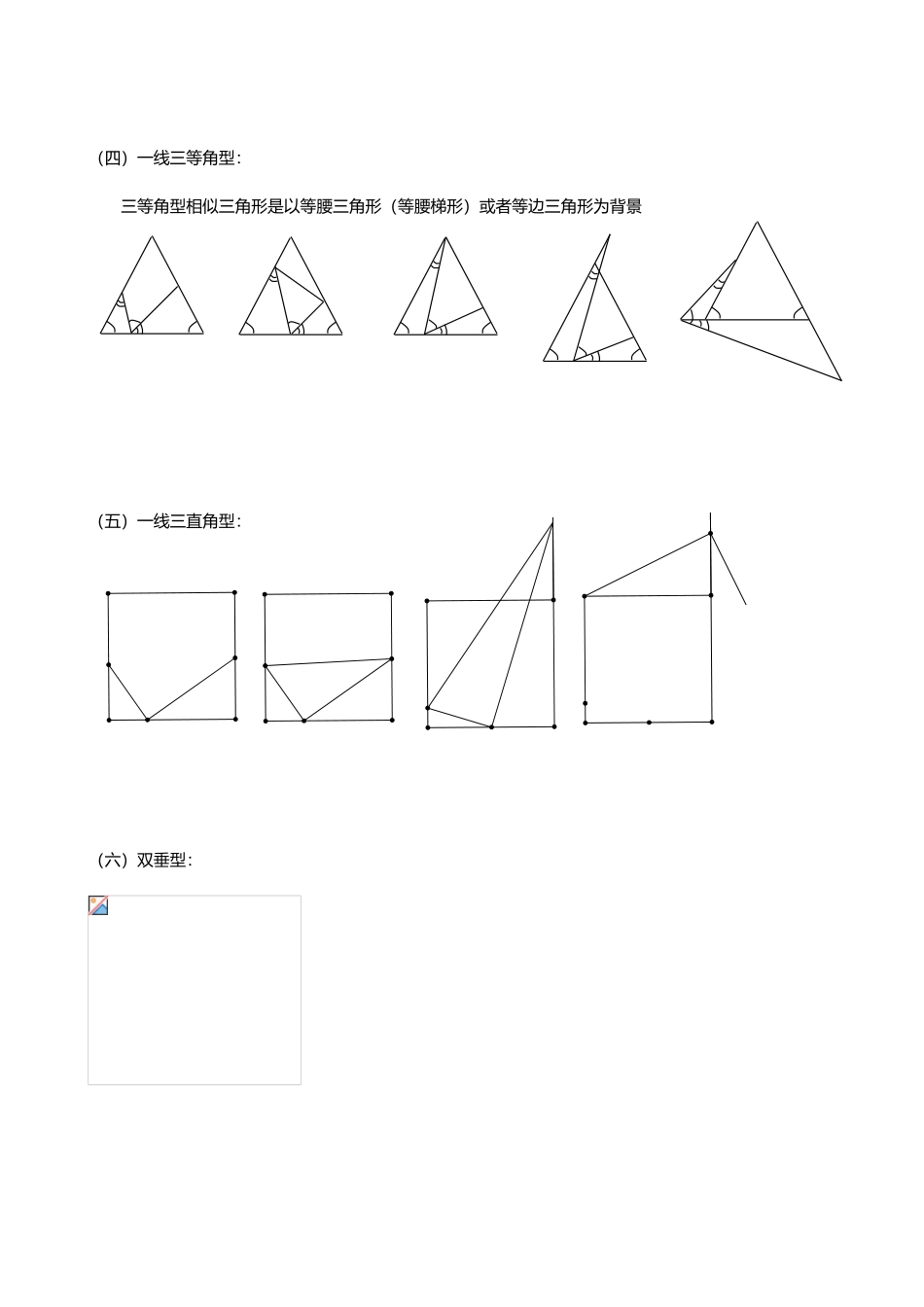
相似三角形模型分析大全一、相似三角形判定的基本模型认识(一)A 字型、反 A 字型(斜 A 字型)ABCDE(平行) CBADE(不平行)(二)8 字型、反 8 字型JOADBCABCD(蝴蝶型) (平行) (不平行)(三)母子型ABCD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:二、相似三角形判定的变化模型旋转型:由 A 字型旋转得到。8 字型拓展共享性GABCEF一线三等角的变形 一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例 1:如图,梯形 ABCD 中,AD∥BC,对角线 AC、BD 交于点 O,BE∥CD 交 CA 延长线于 E. 求证:.例 2:已知:如图,△ABC 中,点 E 在中线 AD 上,.求证:(1); (2).例 3:已知:如图,等腰△ABC 中,AB=AC,AD⊥BC 于 D,CG∥AB,BG 分别交 AD、AC 于 E、F.ACDEB求证:.相关练习:1、如图,已知 AD 为△ABC 的角平分线,EF 为 AD 的垂直平分线.求证:.2、已知:AD 是 Rt△ABC 中∠A 的平分线,∠C=90°,EF 是 AD 的垂直平分线交 AD 于 M,EF、BC 的延长线交于一点 N。求证:(1)△AME∽△NMD; (2)ND =NC·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD⊥AB 于 D,E 是 AC 上一点,CF⊥BE 于 F。求证:EB·DF=AE·DB4.在中,AB=AC,高AD与BE交于H,,垂足为F,延长AD到G,使DG=EF,M是AH的中点。 求证:5.(本题满分 14 分,第(1)小题满分 4 分,第(2)、(3)小题满分各 5 分)已知:如图,在 Rt△ABC 中,∠C=90°,BC=2,AC=4,P 是斜边 AB 上的一个动点,PD⊥AB,交边 AC 于点 D(点 D 与点 A、C 都不重合),E 是射线 DC 上一点,且∠EPD=∠A.设 A、P 两点的距离为 x,△BEP 的面积为 y.(1)求证:AE=2PE;(2)求 y 关于 x 的函数解析式,并写出它的定义域;(3)当△BEP 与△ABC 相似时,求△BEP 的面积.ACBPDE(第 25 题图)双垂型1、如图,在△ABC 中,∠A=60°,BD、CE 分别是 AC、AB 上的高求证:(1)△ABD∽△ACE;(2)△ADE∽△ABC;(3)BC=2ED2、如图,已知锐角△ABC,AD、CE 分别是 BC、AB 边上的高,△ABC 和△BDE 的面积分别是 27 和3,DE=6,求:点 B 到直线 AC 的距离。共享型相似三角形1、△ABC 是等边三角形,D、B、C、E 在一条直线上,∠DAE=,已知 BD=1,CE=3,...