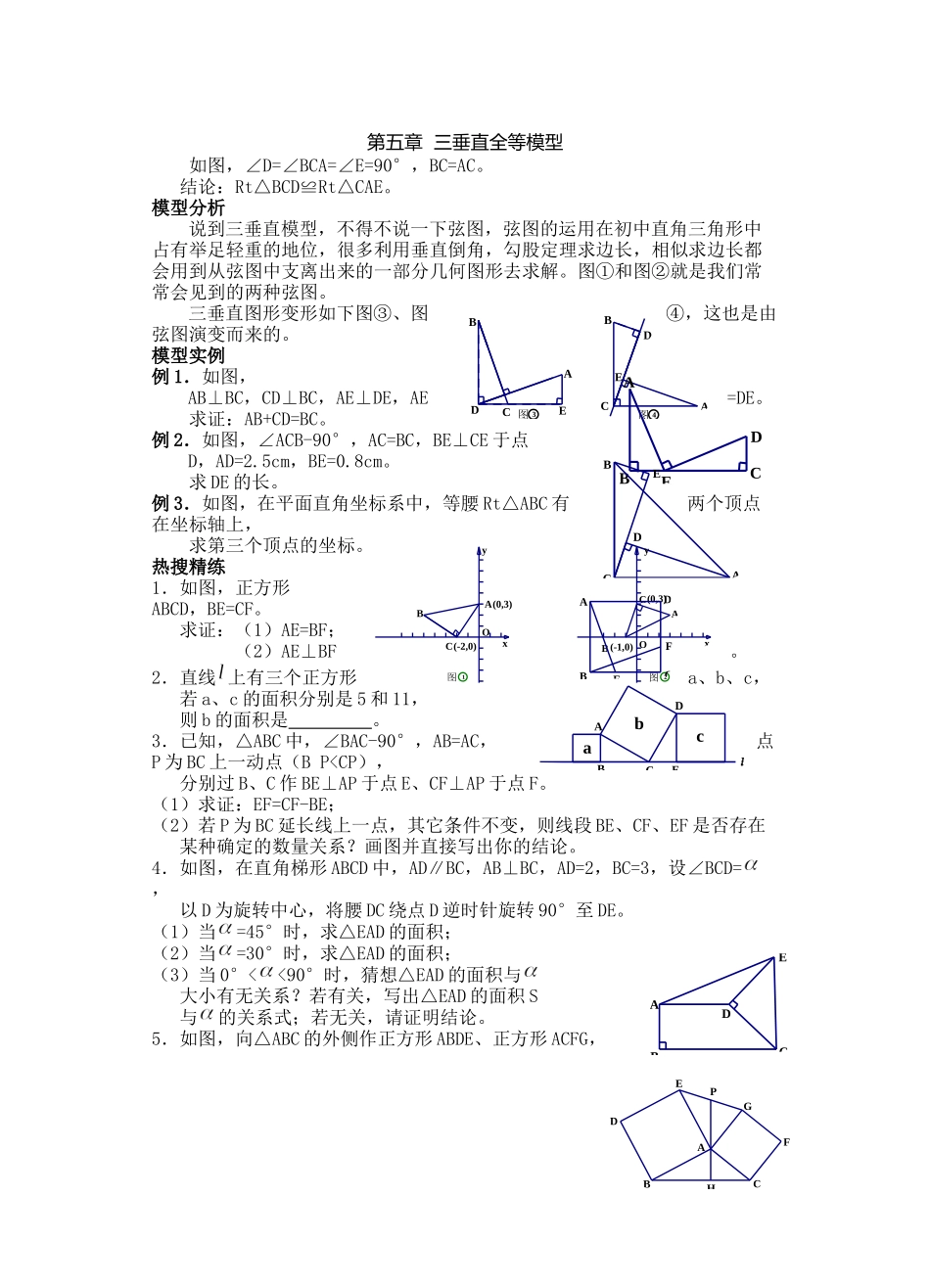
第五章 三垂直全等模型 如图,∠D=∠BCA=∠E=90°,BC=AC。 结论:Rt△BCD≌Rt△CAE。模型分析说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直倒角,勾股定理求边长,相似求边长都会用到从弦图中支离出来的一部分几何图形去求解。图①和图②就是我们常常会见到的两种弦图。三垂直图形变形如下图③、图④,这也是由弦图演变而来的。模型实例例 1.如图,AB⊥BC,CD⊥BC,AE⊥DE,AE=DE。 求证:AB+CD=BC。例 2.如图,∠ACB-90°,AC=BC,BE⊥CE 于点D,AD=2.5cm,BE=0.8cm。 求 DE 的长。例 3.如图,在平面直角坐标系中,等腰 Rt△ABC 有两个顶点在坐标轴上, 求第三个顶点的坐标。热搜精练1.如图,正方形ABCD,BE=CF。 求证:(1)AE=BF;(2)AE⊥BF。2.直线 上有三个正方形a、b、c, 若 a、c 的面积分别是 5 和 11,则 b 的面积是 。3.已知,△ABC 中,∠BAC-90°,AB=AC,点P 为 BC 上一动点(B P