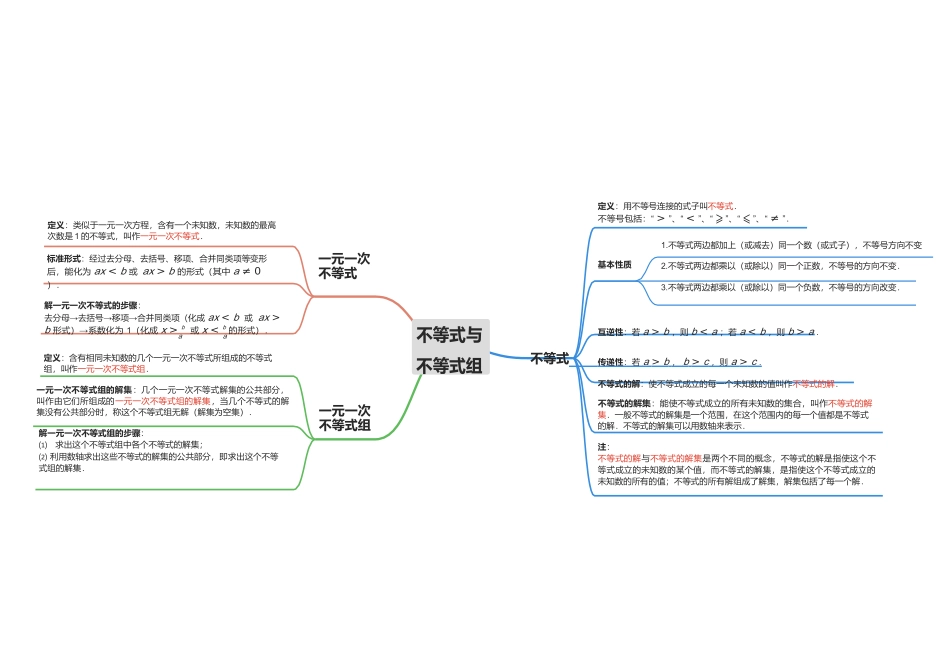
aa定义:类似于一元一次方程,含有一个未知数,未知数的最高次数是 1 的不等式,叫作一元一次不等式.定义:用不等号连接的式子叫不等式.不等号包括:“ > ”、“ < ”、“ ⩾ ”、“ ⩽ ”、“ ≠ ”.1.不等式两边都加上(或减去)同一个数(或式子),不等号方向不变标准形式:经过去分母、去括号、移项、合并同类项等变形 后,能化为 ax < b 或 ax > b 的形式( 其中 a ≠ 0 ).解一元一次不等式的步骤:去分母→去括号→移项→ 合并同类项(化成 ax < b 或 ax >一元一次不等式基本性质2.不等式两边都乘以(或除以)同一个正数,不等号的方向不变.3.不等式两边都乘以(或除以)同一个负数,不等号的方向改变.b 形式)→ 系数化为 1 (化成 x > b 或 x < b 的形式).不等式与互逆性 :若 a > b ,则 b < a ;若 a < b ,则 b > a .定义:含有相同未知数的几个一元一次不等式所组成的不等式组,叫作一元一次不等式组.一元一次不等式组的解集:几个一元一次不等式解集的公共部分, 叫作由它们所组成的一元一次不等式组的解集,当几个不等式的解集没有公共部分时,称这个不等式组无解(解集为空集).解一元一次不等式组的步骤: ⑴求出这个不等式组中各个不等式的解集; ⑵ 利用数轴求出这些不等式的解集的公共部分,即求出这个不等式组的解集.一元一次不等式组不等式组不等式 传递性 :若 a > b , b > c ,则 a > c . 不等式的解:使不等式成立的每一个未知数的值叫作不等式的解.不等式的解集:能使不等式成立的所有未知数的集合,叫作不等式的解集.一般不等式的解集是一个范围,在这个范围内的每一个值都是不等式的解.不等式的解集可以用数轴来表示.注:不等式的解与不等式的解集是两个不同的概念,不等式的解是指使这个不等式成立的未知数的某个值,而不等式的解集,是指使这个不等式成立的未知数的所有的值;不等式的所有解组成了解集,解集包括了每一个解.