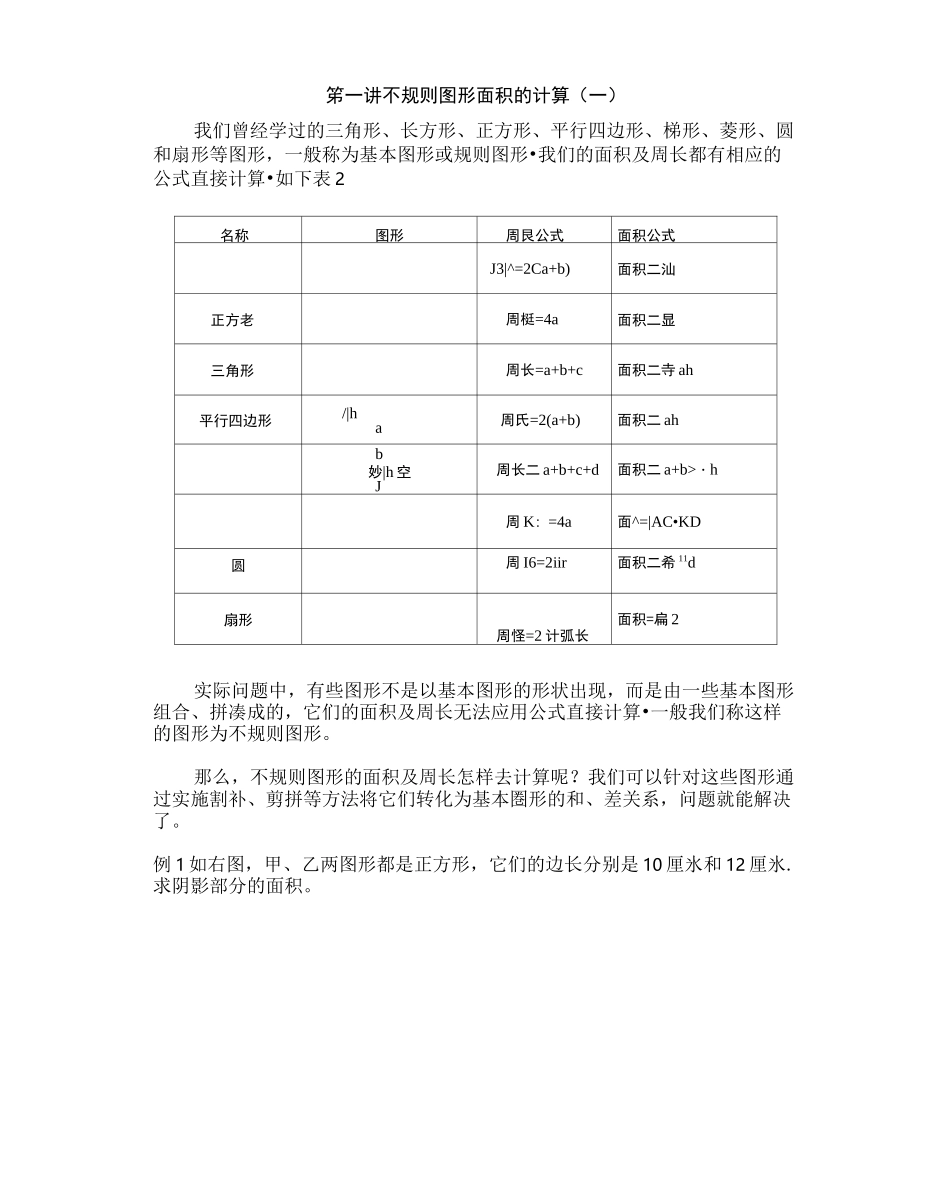
笫一讲不规则图形面积的计算(一)我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形•我们的面积及周长都有相应的公式直接计算•如下表 2名称图形周艮公式面积公式J3|^=2Ca+b)面积二汕正方老周梃=4a面积二显三角形周长=a+b+c面积二寺 ah平行四边形/|ha周氏=2(a+b)面积二 ahb妙|h 空J周长二 a+b+c+d面积二 a+b>・h周 K:=4a面^=|AC•KD圆周 I6=2iir面积二希 11d扇形周怪=2 计弧长面积=扁 2实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算•一般我们称这样的图形为不规则图形。那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本圏形的和、差关系,问题就能解决了。例 1 如右图,甲、乙两图形都是正方形,它们的边长分别是 10 厘氷和 12 厘氷.求阴影部分的面积。k解:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白"三角形仏盹△BDE.△EFG)的面积之和。S^BpE=|(10 十 12)X12=132;仏罰二扌(12J0)"2 二 12。又因为弘+亞二 12X12+10X10 二 244,所以阴影部分面积二 244-(50+132+12)=50(平方厘米)。例 2 如右图,正方形 ABCD 的边长为 6 厘氷,△ABE、△ADF 与四边形 AECF 的面积彼此相竽,求三角形 AEF 的面积.解,因为△ABE、△ADF 与四边形 AECF 的面积彼此相等,所以四边形AECF 的面积与 AABE,ZXADF 的面积都等于正方形 ABCD面积的三分之一.也就是:=S^E=|x6X6=12c在 AABE 中,因为 ABK.所以 BE 二 4,同理 DF 二 4,因此 CE 二 CF 二 2,・'・AECF 的面积为 2x2 一 2 二 2。所以 SZXAEF 二 S 四边形 AECF-SZXECF 二 12-2 二 10(平方厘氷)。蠶器囂辭襦廳蹩蠹边分别是 T 和廿如右图那解:在等腰直角三角形 ABC 中'.'^=10•化磁=*><10X105。又■■■S^c=^SAABC=1x50=25,■;EF=BF=AB-AF=10-6=4,^■■■BEF=7X4X4=8,二阴影部分面积二 SZXABG-S/XBEF 二 25-E7(平方厘米)。例 4 如右图,A 为 ZXCDE 的 DE 边上中点,BC 二 CD,若 ZkABC(阴影部分)面积为 5 平方厘米.求厶旭。及 AACE 的面枳.解:取 BD 中点 F,连结 AF.因为△ADF、AABF 和 ZYABC 等底、等高,所以它们的面积相等,都等于 5 平方厘米.所以△ACD 的面积零于 15...