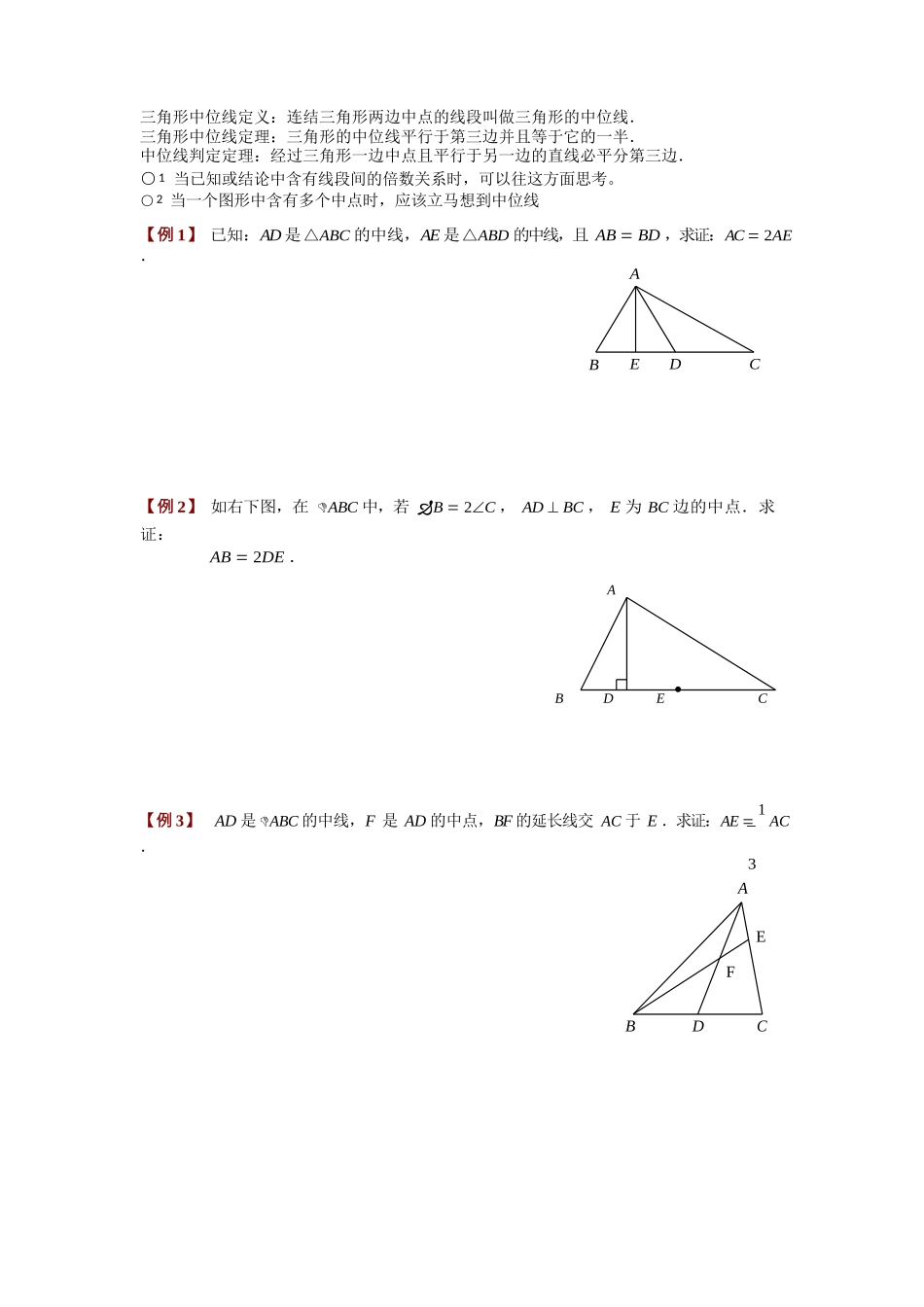
EF三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线. 三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边.○1 当已知或结论中含有线段间的倍数关系时,可以往这方面思考。○2 当一个图形中含有多个中点时,应该立马想到中位线【例 1】 已知:AD 是△ABC 的中线,AE 是△ABD 的中线,且 AB BD ,求证:AC 2AE .ABEDC【例 2】 如右下图,在 ABC 中,若 B 2C , AD BC , E 为 BC 边的中点.求证:AB 2DE .A BDEC【例 3】 AD 是 ABC 的中线,F 是 AD 的中点,BF 的延长线交 AC 于 E .求证:AE 1 AC .3ABDCMFDCNDFCFNM【例 4】 已知,如图四边形 ABCD 中, AD BC , E 、 F 分别是 AB 和 CD 的中点, AD 、EF 、 BC 的延长线分别交于 M 、 N 两点.求证: AME BNE .NAEB【例 5】 已知:在ABC 中,BC AC ,动点 D 绕 ABC 的顶点 A 逆时针旋转,且 AD BC , 连结 DC .过 AB 、 DC 的中点 E 、 F 作直线,直线 EF 与直线 AD 、 BC 分别相交于点 M 、 N .MMDF(N)CCDHAEBAEBAEB图 1图 2图 3(1)如图 1,当点 D 旋转到 BC 的延长线上时,点 N 恰好与点 F 重合,取 AC 的中点 H , 连结 HE 、 HF , 根据三角形中位线定理和平行线的性质, 可得结论AMF BNE (不需证明).(2)当点 D 旋转到图 2 或图 3 中的位置时,AMF 与 BNE 有何数量关系?请分别写出猜想,并任选一种情况证明.FM NEEF【例 6】 已知四边形 ABCD 的对角线 AC BD , E 、F 分别是 AD 、BC 的中点,连结 EF分别交 AC 、 BD 于 M 、 N ,求证:∠AMN ∠BNM .BACD【例 7】 如左下图,在梯形 ABCD 中, AB∥CD , E 、 F 分别是 AC 、 BD 中点.求证:EF ∥ AB ,且 EF 1 AB CD .2D CAB