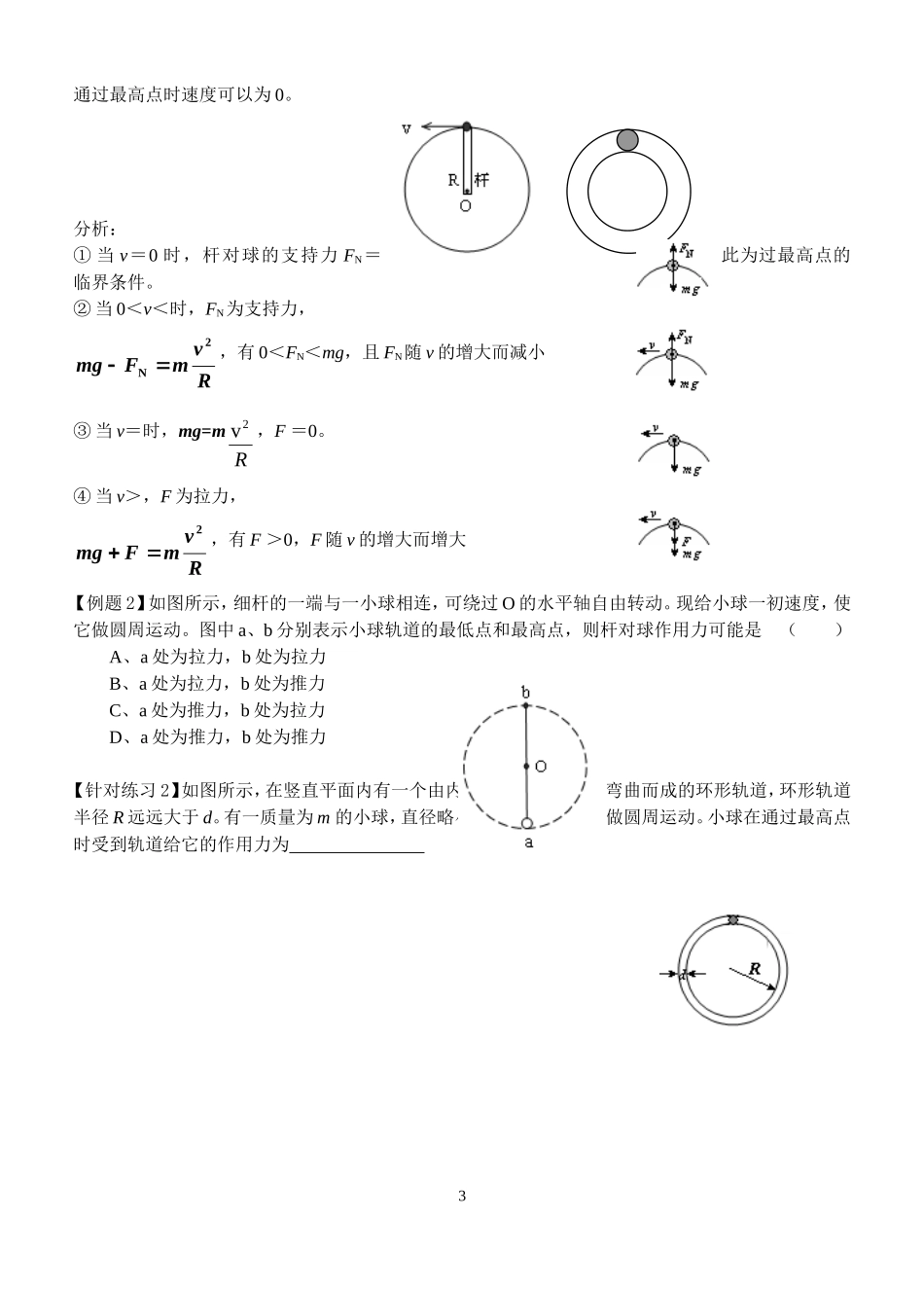
第八节 生活中的圆周运动(第二课时) 1. 知道向心力和向心加速度的公式也适用于变速圆周运动,会求变速圆周运动中物体在特殊点的向心力和向心加速度。2. 会运用受力分析及向心力公式解决圆周运动的临界问题。 1.计算比较在两种不同桥面,桥面受力的情况,设车质量为 m,桥面半径为 R,此时速度为 v。汽车对桥面的压力加速度方向超重失重状态最高点最低点2.向心、圆周、离心运动供需关系何种运动画出大致轨迹rvmF2rvmF2rvmF21二、温故知新一、学习目标【探究一】绳系小球(或内轨道)在竖直平面内的圆周运动如图 1、图 2 所示,没有物体支承的小球,在竖直平面作圆周运动过最高点的情况:对小球进行受力分析如右图所示:由牛顿第二定律得RvmFmg2〖分析〗:① 当 F=0 时(即绳子或轨道对小球没 有 力的作用),v 最小,即Rvmmg2min解得 vmin=,此为小球恰好过最高点的临界速度(最小速度),② 能过最高点的条件:v≥,当 v>时,绳对球产生拉力,轨道对球产生压力。③ 不能过最高点的条件:v<(实际上球没到最高点时就脱离了轨道)。【例题 1】杂技演员在做水流星表演时,用绳系着装有水的碗,在竖直平面内做圆周运动,若水的质量m=0.5 kg,绳长 l=60 cm,求:(1)在最高点时,水不流出的最小速率;(2)水在最高点速率 v=3 m/s 时,水对碗底的压力。【针对练习 1】如图所示,用长为 L 的细绳拴着质量为 m 的小球在竖直平面内做圆周运动,则下列说法中正确的是( )A.小球在圆周最高点时所受的向心力一定为重力B.小球在最高点时绳子的拉力不可能为零C.若小球刚好能在竖直平面内做圆周运动,则其在最高点的速率为gLD.小球过最低点时绳子的拉力一定大于小球重力【探究二】杆系小球(或圆管轨道)在竖直平面内的圆周运动如图所示情形,小球与轻质杆相连。杆与绳不同,它既能施加拉力,也能施加支持力 ,所以小球2四、探究导航v0vR图 2R 绳图 1通过最高点时速度可以为 0。分析:① 当 v=0 时,杆对球的支持力 FN=mg,此为过最高点的临界条件。② 当 0<v<时,FN为支持力, RvmFmg2N ,有 0<FN<mg,且 FN随 v 的增大而减小③ 当 v=时,mg=mR2v,F =0。④ 当 v>,F 为拉力, RvmFmg2,有 F >0,F 随 v 的增大而增大【例题 2】如图所示,细杆的一端与一小球相连,可绕过 O 的水平轴自由转动。现给小球一初速度,使它做圆周运动。图中 a、b 分别...