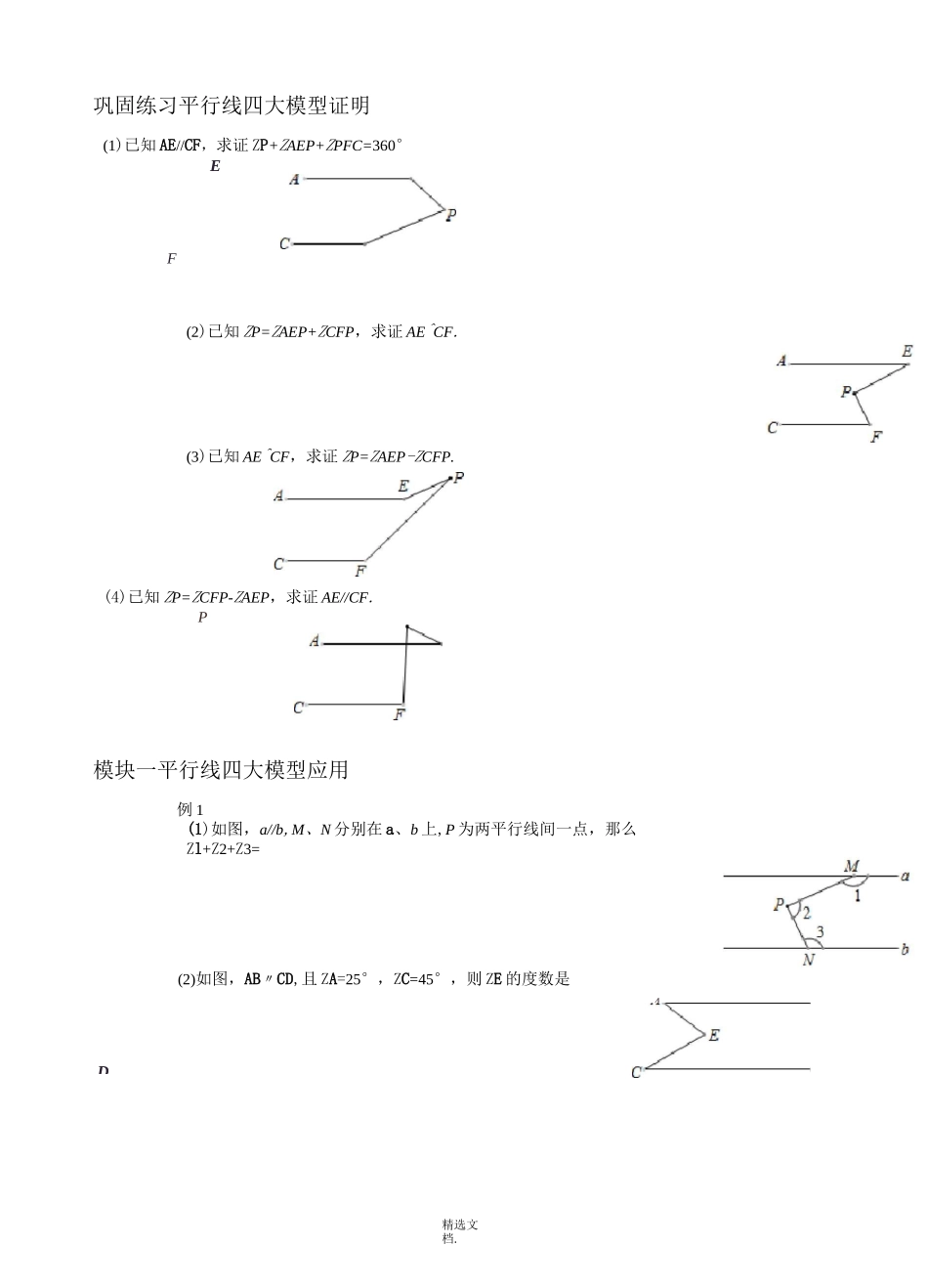
精选文档.平行线四大模型平行线的判定与性质人平行线的判定根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行,但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,这就需要更简单易行的判定方法来判定两直线平行.判定方法 l:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法 2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法 3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知 Z1=Z2,则 AB〃CD(同位角相等,两直线平行);若已知 Z1=Z3,则 AB^CD(内错角相等,两直线平行);若已知 Z1+Z4=180°,则 AB^CD(同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.2、平行线的性质利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果已知两条直线平行,当它们被第三条直线所截,得到的同位角、内错角、同旁内角也有相应的数量关系,这就是平行线的性质.性质 1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质 2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质 3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补精选文档.本讲进阶平行线四大模型模型一“铅笔”模型点 P 在 EF 右侧,在 AB、CD 内部:>“铅笔”模型结论 1:若 AB〃CD,贝 9ZP+ZAEP+ZPFC=360°;结论 2:若 ZP+ZAEP+ZPFC=360°,则 AB〃CD.结论 1:若 AB〃CD,贝 9/P=/AEP+/CFP;结论 2:若 ZP=ZAEP+ZCFP,则 AB^CD.模型二“猪蹄”模型(M 模型)K7D\L/FC点 P 在 EF 左侧,在 AB、CD 内部“猪蹄”模型4D精选文档.巩固练习平行线四大模型证明(1)已知 AE//CF,求证 ZP+ZAEP+ZPFC=360°EF(2)已知 ZP=ZAEP+ZCFP,求证 AE^CF.(3)已知 AE^CF,求证 ZP=ZAEP-ZCFP.(4)已知 ZP=ZCFP-ZAEP,求证 AE//CF.P模块一平行线四大模型应用例 1(1)如图,a//b,M、N 分别在 a、b 上,P 为两平行线间一点,那么Zl+Z2+Z3=(2)如图,AB〃CD,且 ZA=25°,ZC=45°,则 ZE 的度数...