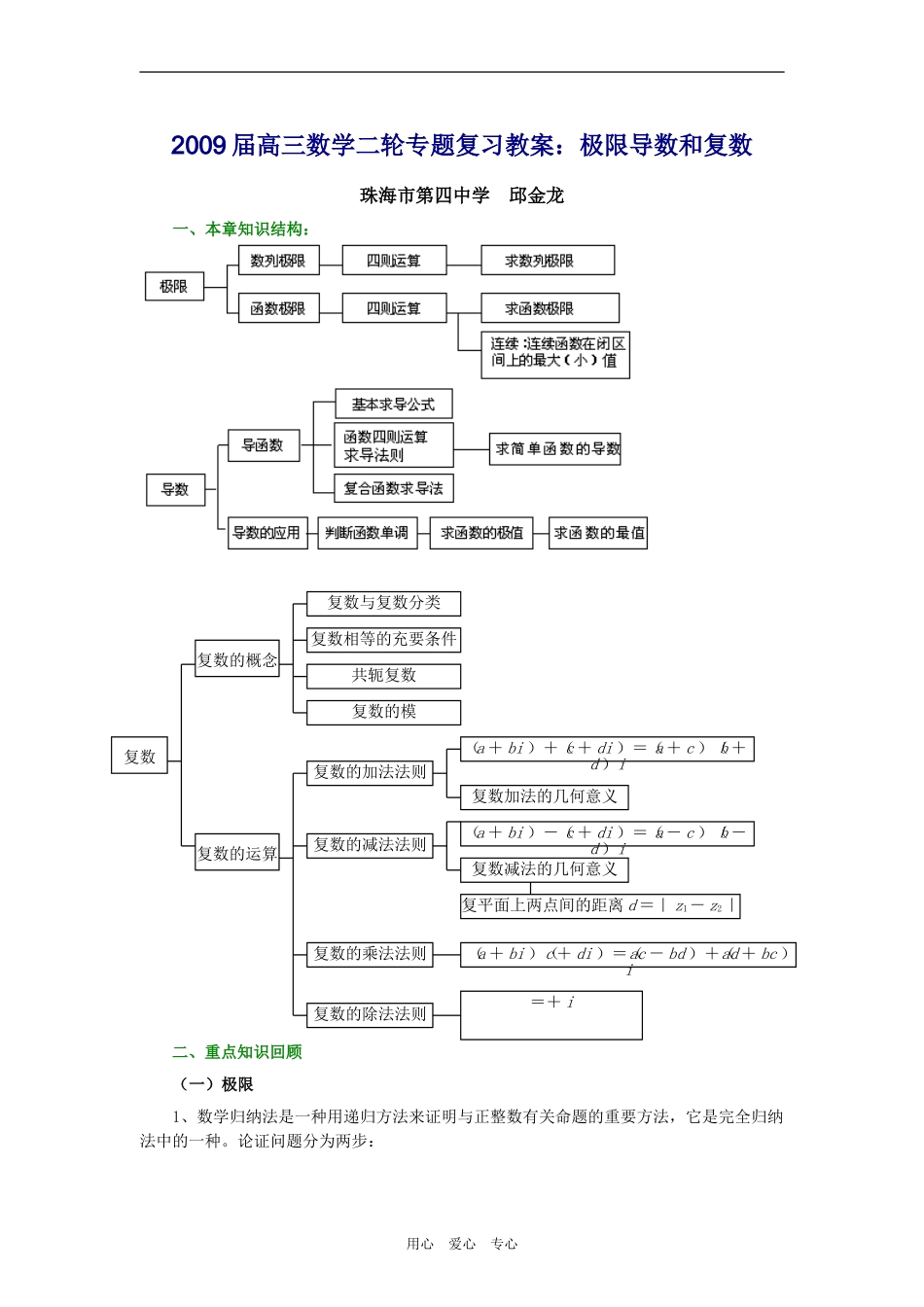
2009 届高三数学二轮专题复习教案:极限导数和复数珠海市第四中学 邱金龙一、本章知识结构:二、重点知识回顾(一)极限1、数学归纳法是一种用递归方法来证明与正整数有关命题的重要方法,它是完全归纳法中的一种。论证问题分为两步:用心 爱心 专心复数复数的概念复数与复数分类复数相等的充要条件共轭复数复数的模复数的运算复数的加法法则复数的减法法则复数的乘法法则复数的除法法则(a + bi )+(c + di )=(a + c )(b +d )i复数加法的几何意义(a + bi )-(c + di )=(a - c )(b -d )i复数减法的几何意义复平面上两点间的距离 d =| z1- z2|(a + bi )(c + di )=(ac - bd )+(ad + bc )i=+ i(1)证明当 n 取第一个值时结论正确;(2)假设当 n=k(k∈且 k≥)时结论正确,证明当 n=k+1 时结论也正确。由(1)、(2)断定命题对于从开始的一切正整数都成立。2、数列极限的定义设是一个无穷数列,A 是一个常数,如果对于预先给定的任意小的正数 ε,总存在正整数 N,使得只要正整数 n>N,就有|-A|<ε,那么就说数列以 A 为极限(或 A 是数列的极限),记作=A。3、数列极限的运算法则如果=A,=B,那么(1) (±)=±=A±B;(2) (·)=·=A·B(3)(4)(c·)= c·=cA(c 为常数)极限运算法则中的各个极限都应存在,都可推广到任意有限个极限的情况,不能推广到无限个。在商的运算法则中,要注意对式子的恒等变形,有些题目分母不能直接求极限。4、特殊数列的极限(1)C=C(C 为常数)(2) 0(|a|<1)= 1(a=l 不存在(|a|>1 或 a=-1)(3) =0(α>0 的常数)(4) (当 k= 时)= 0(当 k< 时 不存在(当 k> 时)用心 爱心 专心说明:欲求极限的式子中,含有项数与 n 有关的“和式”或“积式”,应先求和或积。5、常见的数列极限的类型和求法(1)“”型,分子、分母分别求和再转化。(2)“”型,分子、分母先求和,再化简,转化为有极限。(3)“”型,将其看作分母为 1 的分式,转化求极限。6、与和之间的关系=a ==a。如果在点处左、右极限都存在并且等值,则在点处的极限也存在,并且与左、右极限值相同;如果 在处的左、右极限至少有一个不存在,或者左、右极限都存在但不等值,则函数在点处没有极限,这种关系也反映出、、、也都在处连续。(二)导数1.有关概念① 平均变化率:② 函数在某一点的导数:...