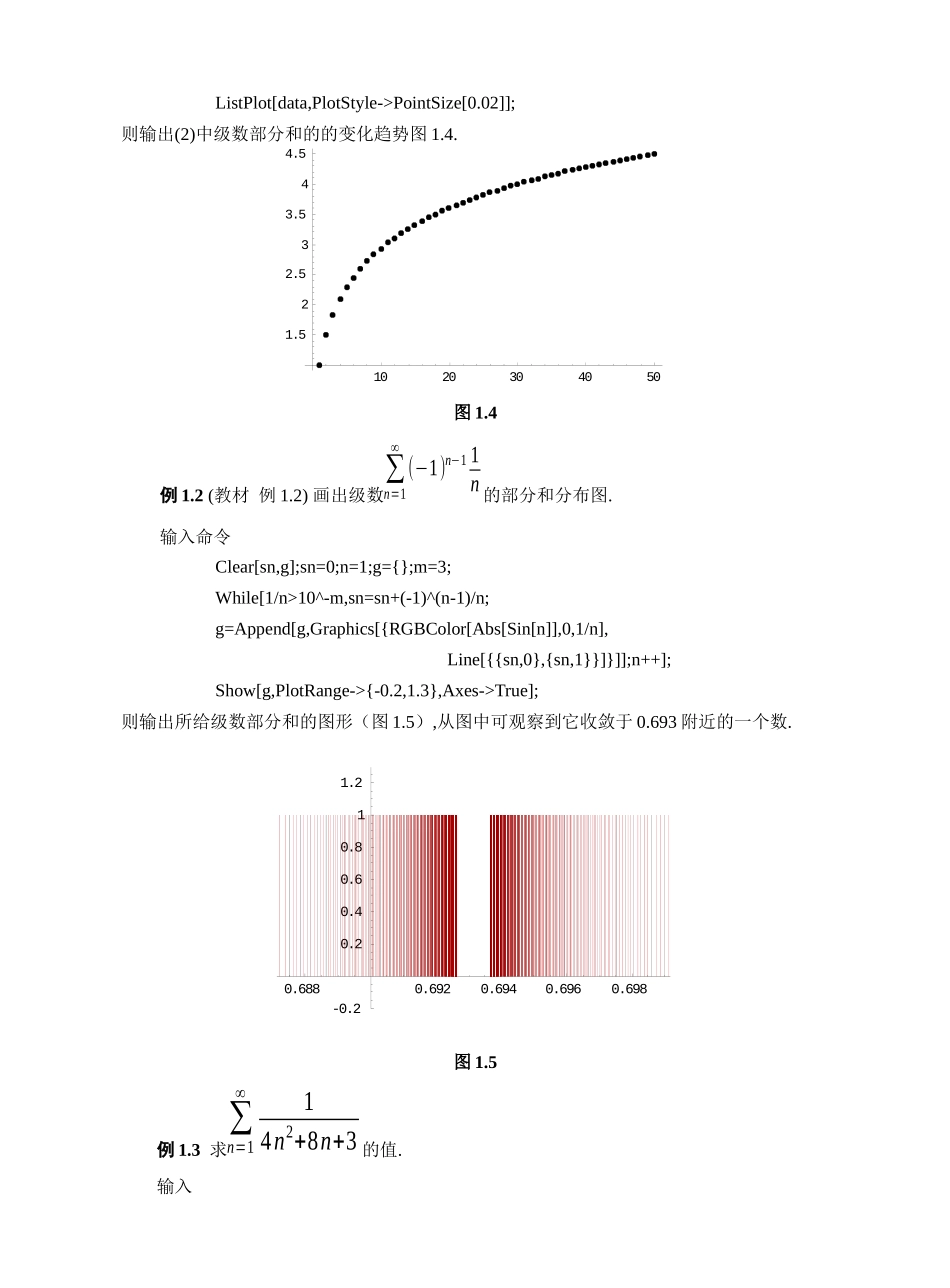
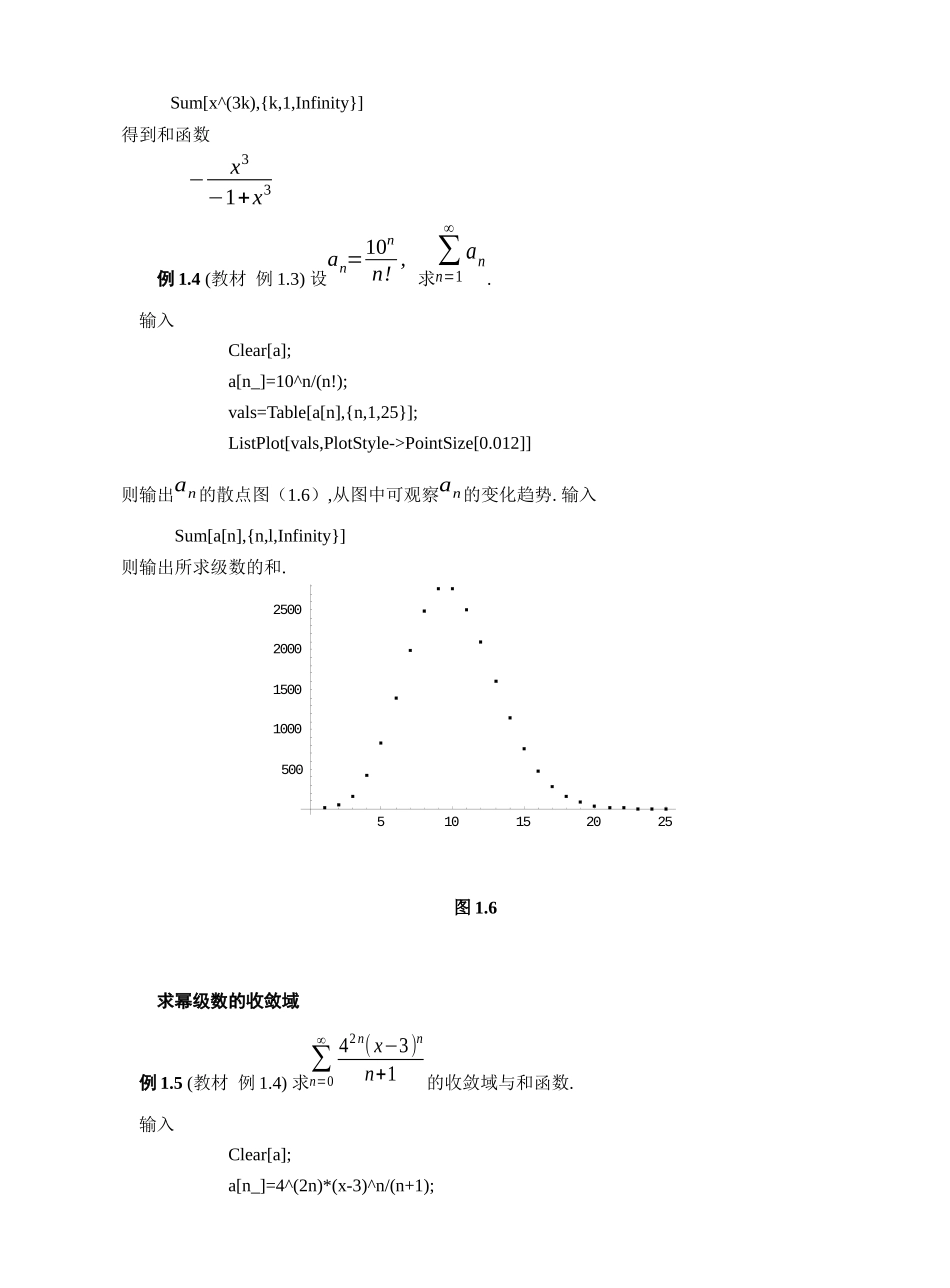
项目四 无穷级数与微分方程 实验 1 无穷级数(基础实验) 实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近. 掌握用 Mathematica 求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法. 数项级数例 1.1 (教材 例 1.1)(1) 观察级数∑n=1∞1n2的部分和序列的变化趋势.(2) 观察级数∑n=1∞ 1n 的部分和序列的变化趋势.输入s[n_]=Sum[1/k^2,{k,n}];data=Table[s[n],{n,100}];ListPlot[data];N[Sum[1/k^2,{k,Infinity}]]N[Sum[1/k^2,{k,Infinity}],40]则输出(1)中级数部分和的变化趋势图 1.3.图 1.3级数的近似值为 1.64493.输入s[n_]=Sum[1/k,{k,n}];data=Table[s[n],{n,50}];204060801001.541.561.581.62ListPlot[data,PlotStyle->PointSize[0.02]];则输出(2)中级数部分和的的变化趋势图 1.4.图 1.4例 1.2 (教材 例 1.2) 画出级数∑n=1∞(−1)n−1 1n 的部分和分布图.输入命令Clear[sn,g];sn=0;n=1;g={};m=3;While[1/n>10^-m,sn=sn+(-1)^(n-1)/n;g=Append[g,Graphics[{RGBColor[Abs[Sin[n]],0,1/n],Line[{{sn,0},{sn,1}}]}]];n++];Show[g,PlotRange->{-0.2,1.3},Axes->True];则输出所给级数部分和的图形(图 1.5),从图中可观察到它收敛于 0.693 附近的一个数.图 1.5例 1.3 求∑n=1∞14n2+8n+3 的值.输入10203040501.522.533.544.50.6880.6920.6940.6960.698-0.20.20.40.60.811.2 Sum[x^(3k),{k,1,Infinity}]得到和函数 −x3−1+x3例 1.4 (教材 例 1.3) 设an=10nn! , 求∑n=1∞an. 输入Clear[a];a[n_]=10^n/(n!);vals=Table[a[n],{n,1,25}];ListPlot[vals,PlotStyle->PointSize[0.012]]则输出an的散点图(1.6),从图中可观察an的变化趋势. 输入 Sum[a[n],{n,l,Infinity}]则输出所求级数的和.图 1.6求幂级数的收敛域 例 1.5 (教材 例 1.4) 求∑n=0∞ 42n(x−3)nn+1的收敛域与和函数. 输入Clear[a];a[n_]=4^(2n)*(x-3)^n/(n+1);5101520255001000150020002500stepone=a[n+1]/a[n]//Simplify则输出 16(1+n)(−3+x)2+n再输入 steptwo=Limit[stepone,n->Infinity]则输出 16(−3+x)这里对 a[n+1]和 a[n]都没有加绝对值. 因此上式的绝对值小于 1 时, 幂级数收敛; 大于 1时发散. 为了求出收敛区间的端点, 输入ydd=Solve[steptwo==1,x]zdd=Solve[steptwo==-1,x]则输出 {{x→4916 }}与{{x→4716 }}由此...