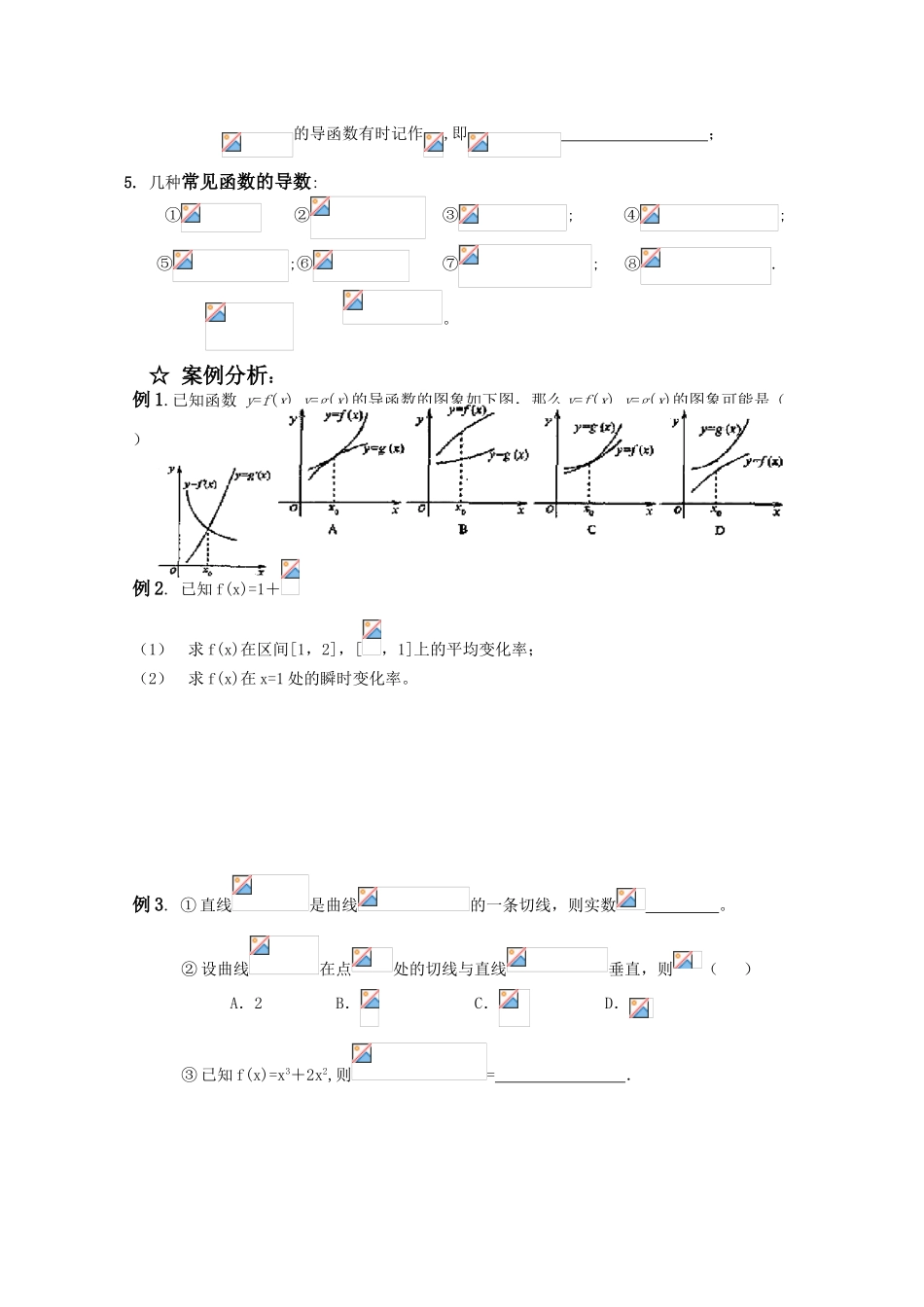
一轮复习学案 §8.1.导数的概念 姓名 ☆复习目标:1.了解导数概念的实际背景,知道瞬时变化率就是导数; 2.通过函数图象直观地理解导数的几何意义.☻基础热身: 1.设 P 为曲线 C:上的点,且曲线 C 在点 P 处切线倾斜角的取 值范围为,则点 P 横坐标的取值范围为( ) A. B. C.D.2. 如图,函数的图象是折线段,其中 的坐标分别为,则 ; .(用数字作答) 3.设曲线在点处的切线与直线垂直, 则 .☻知识梳理:1. 平均变化率: 函数从到的平均变化率= .2. 导数的概念: 函数 y=f(x),如果自变量 x 在 x 处有增量,那么相应地有 10.函数的增量= ; 20.函数的平均变化率= ; 30.若存在, 则称为函数在处的瞬时变化率 也就是 f(x)在点 x 处的导数. 即== .3. 导数的几何意义: 函数在处的导数就是切线的斜率,即= 4. 导函数: 当变化时,便是的一个函数, 称它为的导函数(简称导数), 2BCAyx1O3 4 5 61234 的导函数有时记作,即 ;5. 几种常见函数的导数: ① ② ③; ④;⑤;⑥ ⑦; ⑧. 。 ☆ 案例分析:例 1.已知函数 y=f(x),y=g(x)的导函数的图象如下图,那么 y=f(x),y=g(x)的图象可能是( ) 例 2. 已知 f(x)=1+(1)求 f(x)在区间[1,2],[,1]上的平均变化率; (2)求 f(x)在 x=1 处的瞬时变化率。Ks5u例 3. ① 直线是曲线的一条切线,则实数 。② 设曲线在点处的切线与直线垂直,则( ) A.2 B. C. D.③ 已知 f(x)=x3+2x2,则= . 例 4.设,若函数,有大于零的极值点,则( ) A. B. C. D.例 5.设函数,曲线在点处的切线方程为.(1)求的解析式;(2)证明:曲线上任一点处的切线与直线和直线所围成的三角形面积为定值,并求此定值。Ks5u参考答案:☻基础热身:1.【答案】A【解析】本小题主要考查利用导数的几何意义求切线斜率问题。依题设切点的横坐标为, 且(为点 P 处切线的倾斜角),又 ,∴,∴2. 【标准答案】: 2 -2【试题分析】: f(0)=4,f(4)=2;由导数的几何意义知-2.【高考考点】: 函数的图像,导数的几何意义。【易错提醒】: 概念“导数的几何意义”不清。3. 【答案】 2【解析】,∴切线的斜率,所以由得例 1. 【标准答案】D【试题解析】从导函数的图象可知两个函数在处斜率相同,可以排除 B 答案,再者导函数的函数值反映的是原函数的斜率大小,可明显看出 y=f(x)的导函数的值在减小,所以原...