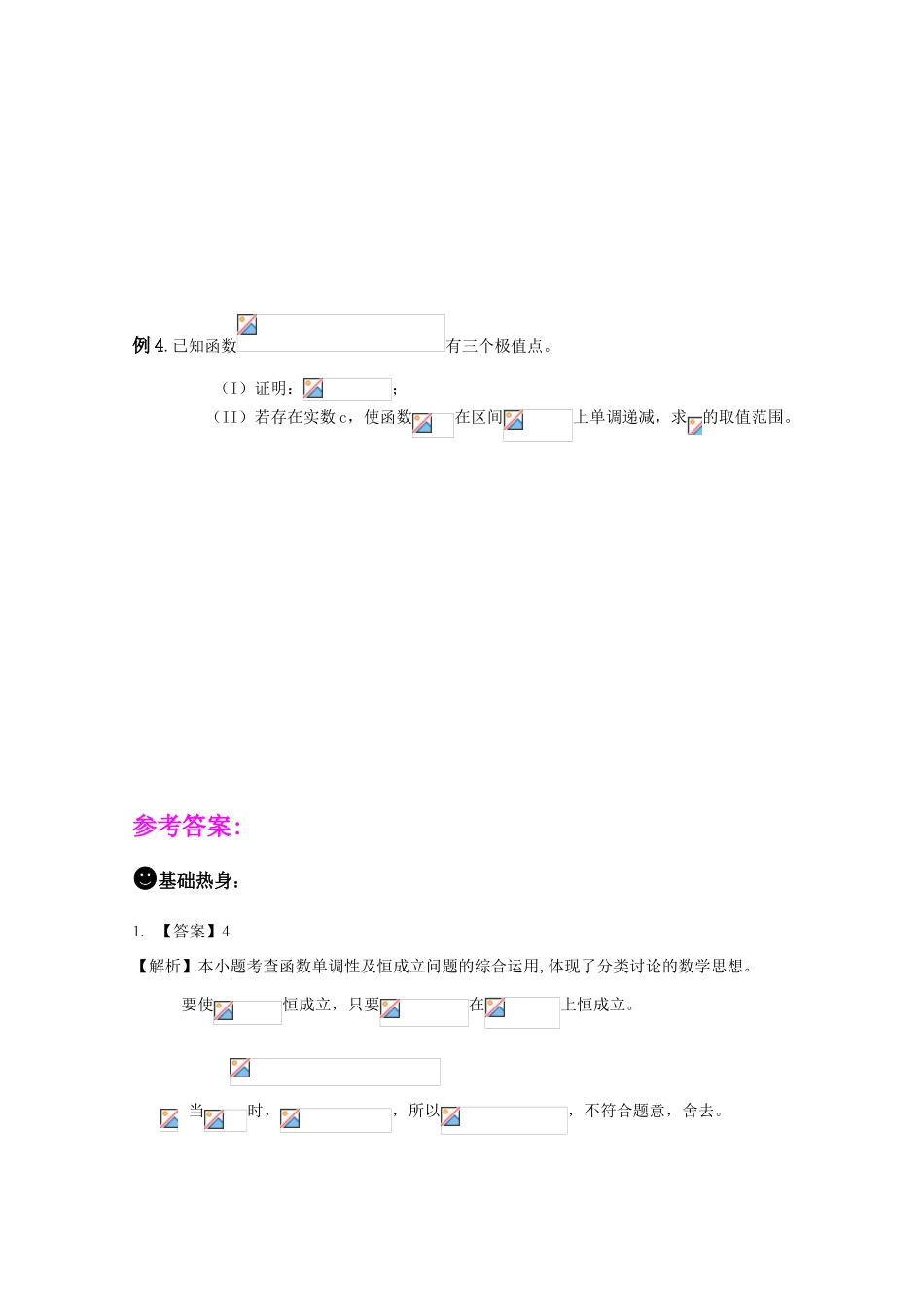
一轮复习学案 §8.3.导数的应用(1) ☆复习目标:1.理解可导函数的单调性与其导数的关系; 2.了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号)。☻基础热身:1. 对于总有成立,则= 。2. 设函数为实数。(Ⅰ)已知函数在处取得极值,求的值; (Ⅱ)已知不等式对任意都成立,求实数的取值范围。☻知识梳理:1.单调性与导数① 若在上恒成立,在 函数若在上恒成立,在 函数② 在区间上是增函数 在上恒成立;在区间上为减函数 在上恒成立.2.极值与导数10. 设函数在点附近有定义,如果左 右 ,则是函数的一个极大值; 如果左 右 ,则是函数的一个极小值; 如果左右不改变符号,那么在这个根处 .注意: ① 极值是一个局部概念,不同与最值; ② 函数的极值不是唯一的; ③极大值与极小值之间大小关系: ;④数的极值点一定出现在区间的内部.20.求可导函数极值的步骤:① ;② ;③ .3.利用导数求函数的最值 设函数在上连续,在内可导,则求在上的最大值与最小值的步骤: ① ;② .☆ 案例分析:例 1.已知函数,且是奇函数.(Ⅰ)求,的值;(Ⅱ)求函数的单调区间.例 2.已知函数,.(Ⅰ)讨论函数的单调区间;Ks5u(Ⅱ)设函数在区间内是减函数,求的取值范围.例 3.已知函数,R 且. (Ⅰ)若曲线在点处的切线垂直于 y 轴,求实数的值; (Ⅱ)当时,求函数的最大值和最小值.例 4.已知函数有三个极值点。Ks5u (I)证明:; (II)若存在实数 c,使函数在区间上单调递减,求的取值范围。参考答案:☻基础热身:1. 【答案】4【解析】本小题考查函数单调性及恒成立问题的综合运用,体现了分类讨论的数学思想。 要使恒成立,只要在上恒成立。当时,,所以,不符合题意,舍去。当时,即单调递减, ,舍去。当时Ks5u① 若时在和 上单调递增,在上单调递减。所以② 当时在上单调递减,,不符合题意,舍去。综上可知 a=4.2. 【解析】(I)在取得极值即(Ⅱ)即 令Ks5u 即对任意都成立则即例 1. 【解析】(Ⅰ)因为函数为奇函数, 所以,对任意的,,即. 又所以. 所以解得.(Ⅱ)由(Ⅰ)得.所以. 当时,由得.变化时,的变化情况如下表:00 所以,当时,函数在上单调递增,在上单调递减, 在上单调递增. 当时,,所以函数在上单调递增.例 2. 【试题解析】 例 3. 解: =Ks5u =. --------------------3 分 (Ⅰ) 曲线在点处的切线垂直于 y 轴, 由...