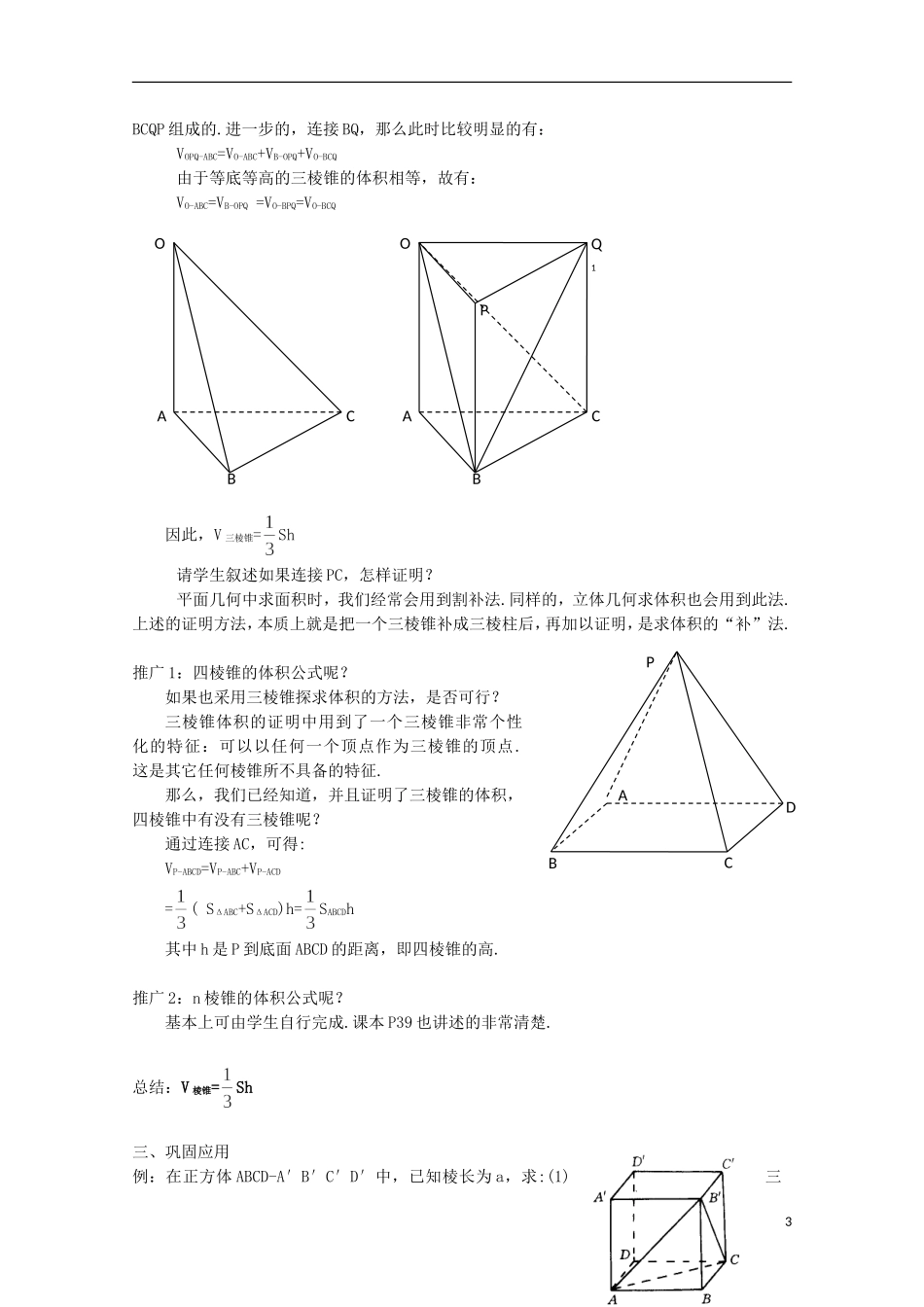
15.5 几何体的体积(2)锥体的体积一、教学内容分析锥体的体积是学习祖暅原理与柱体体积之后,对几何体体积的进一步探索.其中三棱锥体积在这之中又尤为重要,起着承上启下的作用.推导三棱锥的体积要用到前一课时的内容;同时,n 棱锥乃至圆锥的体积公式又是建立在三棱锥体积之上的.所以处理好三棱锥的体积问题,是这堂课的重中之重.二、教学目标设计学生通过具体实验感知三棱锥体积公式,通过严谨证明确认三棱锥体积公式,通过对新知识的应用推广得到 n 棱锥的体积公式,通过具体实例初步应用锥体体积公式.能应用割补法求体积以及体积法求点到面的距离,在这个过程中,提高分析、综合、抽象、概括等逻辑推理能力.三、教学重点及难点三棱锥体积公式及其探求.四、教学流程设计五、教学过程设计一、情景引入1、复习祖暅原理:体积可看成是有面积叠加而成,用一组平行平面截两个空间图形,若在任意等高处的截面面积都对应相等,则两空间图形的体积必然相等.2、柱体体积公式:V 棱柱=Sh3、问题:锥体的体积公式是什么?会不会和柱体的体积有什么联系?实验:如图取一个三棱锥教具(无底面 ABC),一个与之同底等高的三棱柱教具(无底面 ABC)(教具可用硬板纸制作),以及黄沙若干.复习已学知识做好上课准备通过实验发现规律提出质疑严谨证明继续推广特殊到一般简单应用巩固公式课堂小结布置作业1用三棱锥盛满黄沙,倒入三棱柱容器中,发现倒三次正好把三棱柱容器填满.从这个实验中,学生猜想三棱锥的体积公式为 V 三棱锥=Sh这个实验的结果到底是一个美丽的巧合还是一个必然的结果?二、学习新课问题 1:从猜想的三棱锥体积公式为 V 三棱锥=Sh 看,体积只和三棱锥底面积和高有关,而与底面三角形的形状无关.那么,上述实验中的三棱柱不变,三棱锥变成与原三棱锥 O-ABC 等底等高的三棱锥 P-DEF,结果是否会不变呢?解决此问题,即要证明等底等高的三棱锥的体积相等.已知三棱锥 O-ABC 和 P-DEF 的底面积都是 S,高都是 h.求证:三棱锥 O-ABC 和 P-DEF 的体积相等.证明:把两个三棱锥的底面都放在平面上,任意作平面,设平面截三棱锥 O-ABC 所得的截线为三角形 A’B’C’,其面积为 S1;平面截三棱锥 P-DEF 所得的截线为三角形 D’E’F’,其面积为 S2.如果三棱锥的顶点 O 和 P 与平面的距离为 h1,那么推得:和,于是得,相似比是,同理可得,相似比也是.由相似形的性质得,.即.因为任意平行于底面的平面截两个三棱...