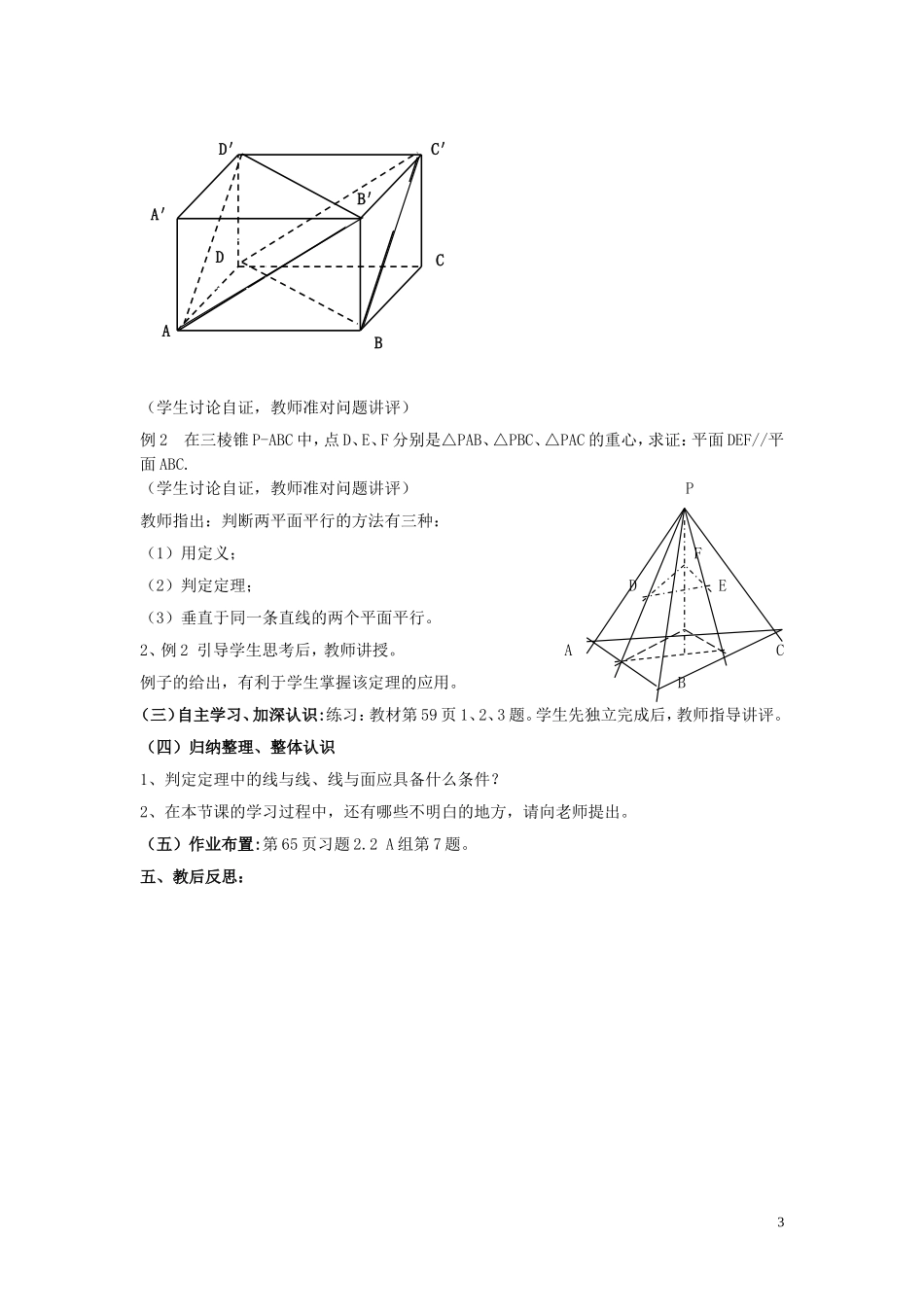
第十课时§2.2.2 平面与平面平行的判定一、教学目标:1、知识与技能:理解并掌握两平面平行的判定定理。2、过程与方法:让学生通过观察实物及模型,得出两平面平行的判定。3、情感、态度与价值观:进一步培养学生空间问题平面化的思想。二、教学重点、难点:重点:两个平面平行的判定。难点:判定定理、例题的证明。三、学法与教法1、学法:学生借助实物,通过观察、类比、思考、探讨,教师予以启发,得出两平面平行的判定。2、教法:探究讨论法四、教学过程(一)创设情景、引入课题引导学生观察、思考教材第 57 页的观察题,导入本节课所学主题。(二)研探新知问题提出:1.空间两个不同平面的位置关系有哪几种情况?2.两个平面平行的基本特征是什么?有什么简单办法判定两个平面平行呢?知识探究(一):平面与平面平行的背景分析 思考 1:根据定义,判定平面与平面平行的关键是什么?思考 2: 若一个平面内的所有直线都与另一个平面平行,那么这两个平面的位置关系怎样?若一个平面内有一条直线与另一个平面有公共点,那么这两个平面的位置关系又会怎样呢?思考 3:三角板的一条边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?思考 4:三角板的两条边所在直线分别与桌面平行,三角板所在平面与桌面平行吗?思考 5:一般地,如果平面 α 内有一条直线平行于平面 β,那么平面 α 与平面 β 一定平行吗?如果平面 α 内有两条直线平行于平面 β,那么平面 α 与平面 β 一定平行吗?αβ1知识探究(二):平面与平面平行的判定定理 思考 1:对于平面 α、β,你猜想在什么条件,下可保证平面 α 与平面 β 平行?思考 2:设 a,b 是平面 α 内的两条相交直线,且 a//β,b//β. 在此条件下,若 α∩β=l ,则直线 a、b 与直线 l 的位置关系如何?思考 3:通过上述分析,我们可以得到判定平面与平面平行的一个定理,你能用文字语言表述出该定理的内容吗?再通过长方体模型, 引导学生观察、思考、交流,得出结论。两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。符号表示:a βb βa∩b = P β∥α则 a∥α b∥α例1 在正方体 ABCD-A′B′C′D′中. 求证:平面 AB′D′∥平面 BC′D. αβabαβl2(学生讨论自证,教师准对问题讲评)例 2 在三棱锥 P-ABC 中,点 D、E、F 分别是△PAB、△PBC、△PAC 的重心,求证:平面 DEF//平面 ABC....