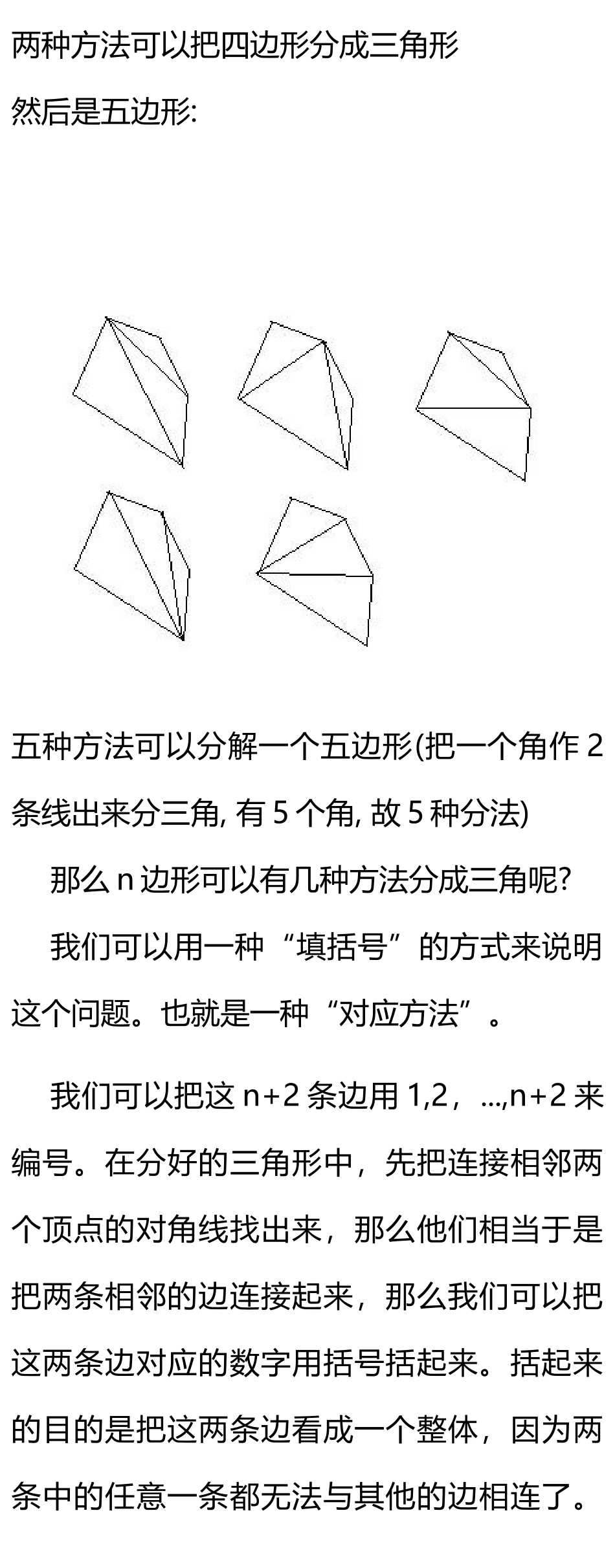
无处不在的卡特兰数亲爱的小伙伴们晚上好哟!继昨天的仿射变换之后,今日又是讨论组合数学问题的时候了。今日我们要来看的是一个奇妙的数列,为了纪念比利时数学家卡特兰而把它叫做卡特兰(catalan)数.这个数列是卡特兰在讨论凸 n 边形的剖时得到的。凸 n+2 边形用其 n-1 条对角线把此凸 n+2 边形分割为互不重叠的三角形,这种分法的总数为 Tn。据说有几十种看上去毫不相干的组合计数问题的最终表达式都是卡特兰数的形式。那么我们首先来回到卡特兰的时代,看一看这个数列的通项是怎么求解出来的吧。我们用几个例子开始阐述问题:首先是三角形, 只有一种方法分成三角形..就是什么都不做。 然后是四边形:两种方法可以把四边形分成三角形然后是五边形:五种方法可以分解一个五边形(把一个角作 2条线出来分三角, 有 5 个角, 故 5 种分法)那么 n 边形可以有几种方法分成三角呢?我们可以用一种“填括号”的方式来说明这个问题。也就是一种“对应方法”。我们可以把这 n+2 条边用 1,2,...,n+2 来编号。在分好的三角形中,先把连接相邻两个顶点的对角线找出来,那么他们相当于是把两条相邻的边连接起来,那么我们可以把这两条边对应的数字用括号括起来。括起来的目的是把这两条边看成一个整体,因为两条中的任意一条都无法与其他的边相连了。在图形上,我们可以这样操作:把括起来的两条边擦掉,然后把连接他们的对角线看成新的边,然后在这些边中继续上面的操作。比如上面这张图就可以这样表示:1(((23 ) 4)(56))那么从最后一个数(n+2)开始数起,数字的个数至少要比左括号(“(”)的个数多 1:这是因为边之间连线为两个数字添一个括号,对角线与边连线相当于增加 1 个数字和增加一个括号。而我们知道 n+2 条边有 n-1 条对角线,我们假如把刚才的数字记成 1(也就是边的个数),把刚才的左括号(注意我们不考虑右括号是因为左括号确定以后右括号的补法是唯一确定的,并且左括号的个数比对角线个数多 1)记成-1,那么上面这种排列就成了1 -1 -1 -1 1 1 1 -1 1 1 于是这个问题又变成了 n 个-1 和 n+2 个 1排列,并且从右边数 1 的个数始终多于-1 的情况数。慢着,我们先回顾一下:刚才我们在分三角形,最后怎么变成排-1 和 1 了?这就是前文所说的“对应方法”:分三角形也好,填括号也好,排-1 和 1 也好,这三种不同的情景实际上是同一个问题的边形,它们所有可能的情况数是一模一...