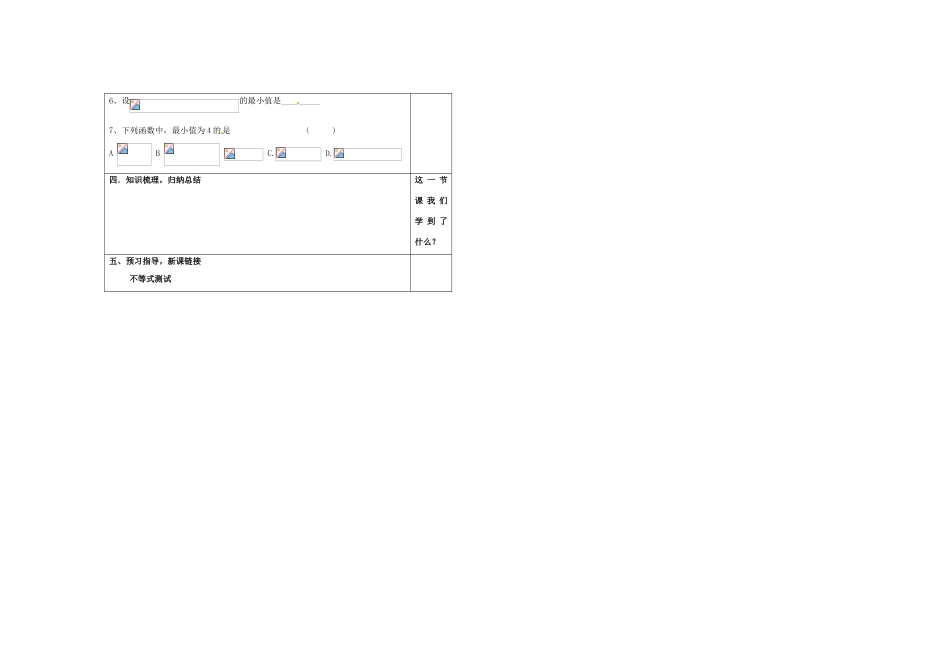
授课时间 年 月 日第 周星期编号课题基本不等式及其应用课型复习知识目标掌握基本不等式及其常见变形能力目标能利用基本不等式求最值情感态度与价值观让学生获得掌握方法的成就感,进而激发学习数学的热情学习重点利用基本不等式求最值学习难点利用基本不等式求综合问题导学设计一.学情调查,情景导入1、基本不等式成立的条件是:2、基本不等式的两个变形:(1) (2) 3、基本不等式求最值:(1)积定和最小; (2)和定积最大二.问题展示,合作探究探究类型一:利用基本不等式证明例 1、已知 x>0,y>0,z>0.求证:≥8练:已知,,求证:探究类型二:利用基本不等式求最值例 2、(1)x+3y-2=0,则 3x+27y+1 的最小值为 .(2)x,y,z∈R+,x-2y+3z=0, 的最小值是 .练:设,若是与的等比中项,则的最小值是 .思考:类型一与类型二是否都需要考虑取等号的条件?探究类型三:利用基本不等式解应用问题例 3、某 造纸厂拟建一座平面图形为矩形且面积为 162 平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为 400 元/米,中间两道隔墙建造单价为 248 元/米,池底建造单价为 80 元/米 2,水池所有墙的厚度忽略不计.(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;(2)若由于地形 限制,该池的长 和宽都不能超过 16 米,试设计污水池的长和宽,使总造价最低,并求出最低总造价.。三. 达标训练,巩固提升1、已知 a,b,c 均为正数,且 a+b+c=1,求证:++≥9.2、已知 x>0,y>0,且+=1,求 x+y 的最小值;3、已知 x<,求函数 y=4x-2+的最大值;4、若且,则下列四个数中最大的是( )A. B. C.2ab D.a 5、设 x>0,则的最大值为_______6、设的最小值是_________7、下列函数中,最小值为 4 的是 ( )A B C. D.四.知识梳理,归纳总结这 一 节课 我 们学 到 了什么?五、预习指导,新课链接不等式测试