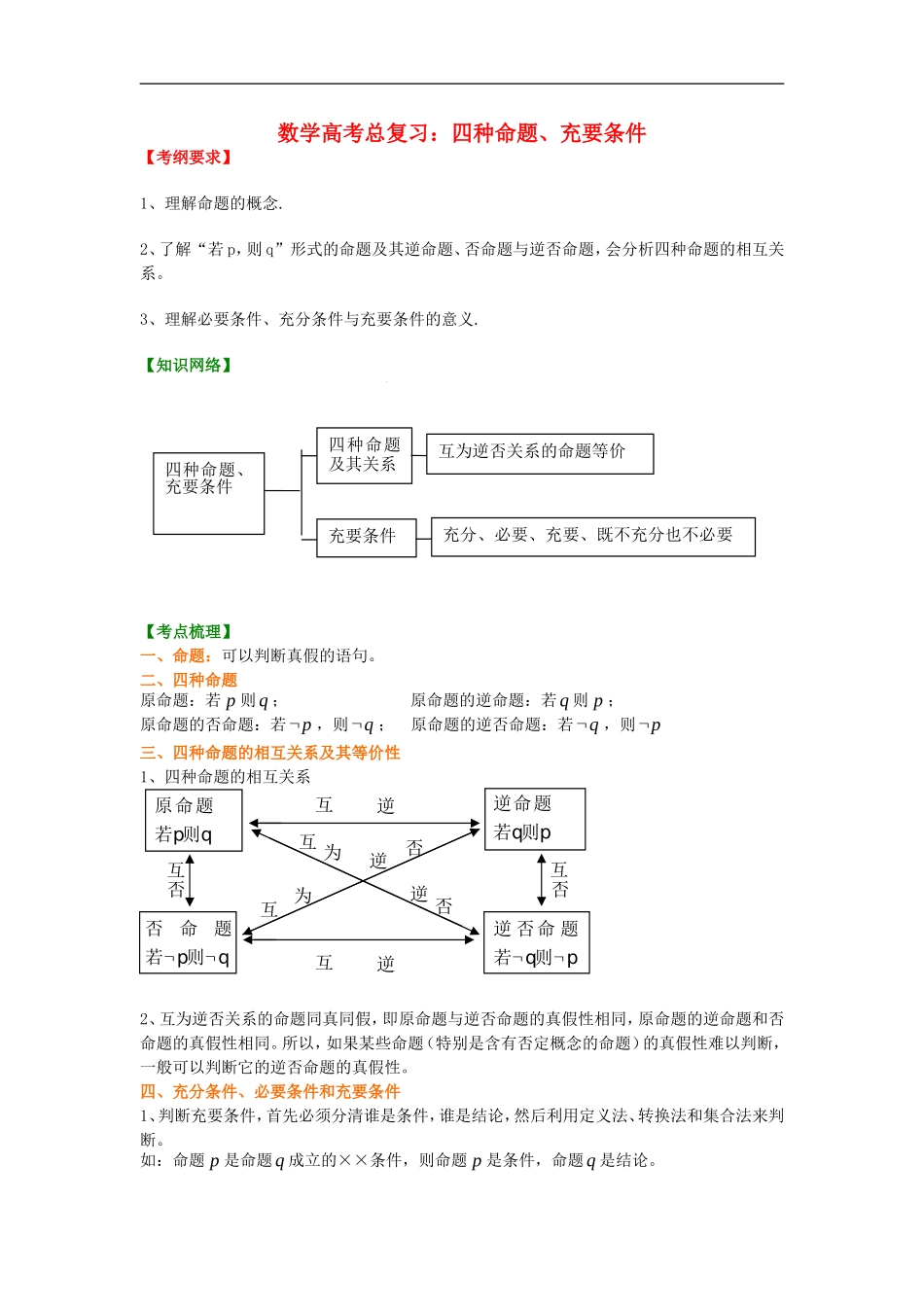
数学高考总复习:四种命题、充要条件【考纲要求】1、理解命题的概念.2、了解“若 p,则 q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系。3、理解必要条件、充分条件与充要条件的意义.【知识网络】【考点梳理】一、命题:可以判断真假的语句。二、四种命题原命题:若 p 则q ; 原命题的逆命题:若q 则 p ;原命题的否命题:若p,则q; 原命题的逆否命题:若q,则p三、四种命题的相互关系及其等价性1、四种命题的相互关系2、互为逆否关系的命题同真同假,即原命题与逆否命题的真假性相同,原命题的逆命题和否命题的真假性相同。所以,如果某些命题(特别是含有否定概念的命题)的真假性难以判断,一般可以判断它的逆否命题的真假性。四、充分条件、必要条件和充要条件1、判断充要条件,首先必须分清谁是条件,谁是结论,然后利用定义法、转换法和集合法来判断。如:命题 p 是命题q 成立的××条件,则命题 p 是条件,命题q 是结论。互逆否命题若 p则 q原命题若p则q逆命题若q则p逆 否命 题若 q则 p互逆互逆否为互逆 否为否否互互四种命题、充要条件充要条件四种命题及其关系互为逆否关系的命题等价充分、必要、充要、既不充分也不必要又如:命题 p 成立的××条件是命题q ,则命题q 是条件,命题 p 是结论。又如:记条件 ,p q 对应的集合分别为 A,B 则 AB,则 p 是q 的充分不必要条件; AB,则 p 是q 的必要不充分条件。2、“ ”读作“推出”、“等价于”。 pq,即 p 成立,则q 一定成立。3、充要条件已知命题 p 是条件,命题q 是结论(1)充分条件:若 pq,则 p 是q 充分条件.所谓“充分”,意思是说,只要这个条件就够了,就很充分了,不要其它条件了。如:3x 是4x 的充分条件。(2)必要条件:若qp,则 p 是q 必要条件.所谓“必要”,意思是说,这个条件是必须的,必要的,当然,还有可能需要其它条件。如:某个函数具有奇偶性的必要条件是其定义域关于原点对称。函数要具有奇偶性首先必须定义域关于原点对称,否则一定是非奇非偶。但是定义域关于原点对称并不就一定是奇偶函数,还必须满足)()(xfxf才是偶函数,满足)()(xfxf是奇函数。(3)充要条件:若 pq,且qp,则 p 是q 充要条件.【典型例题】类型一:四种命题及其关系例 1. 写出命题“已知 ,a b 是实数,若 ab=0,则 a=0 或 b=0”的逆命题,否...