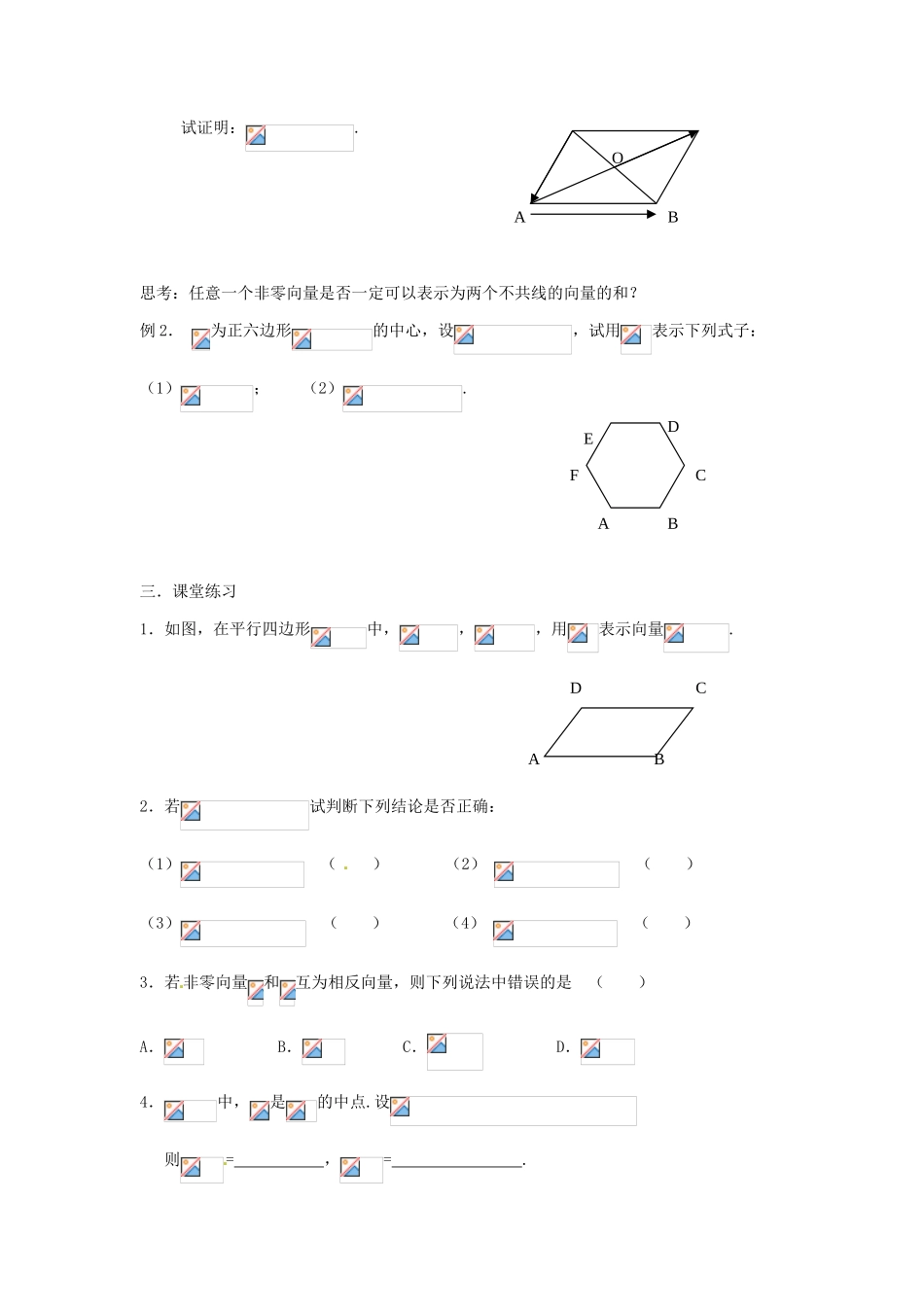
安徽省安庆市第九中学 2013 届高三数学总复习《第三课时 向量的减法》学案一. 问题情境:数能进行运算,向量也能进行运算,在数的运算中,减法运算是加运算的逆运算,那么向量的减法运算呢?二.建构数学:向量的减法是向量加法的逆运算.1.若,则向量叫做与的差,记为__________,求两个向量差的运算,叫做向量的__________.根据向量减法的定义和向量加法的三角形法则,我们可以得到向量的作图方法.如图,已知向量和不共线,求作向量. 这就是说,当向量, ____ 时,从 的____点指向 的___点的向量就是 .(首同尾连,指向被减)思考:如果,怎样作出呢?由向量加法的结合律可知, 所以 . 这表明:减去一个向量等于加上这个向量的________向量.思考:你能画图说明吗?二.数学应用例 1.如图,是平行四边形的对角线的交点,若,CDBOA试证明:.思考:任意一个非零向量是否一定可以表示为两个不共线的向量的和?例 2. 为正六边形的中心,设,试用表示下列式子:(1); (2).三.课堂练习1.如图,在平行四边形中,,,用表示向量. 2.若试判断下列结论是否正确:(1) ( ) (2) ( )(3) ( ) (4) ( )3.若非零向量和互为相反向量,则下列说法中错误的是 ( )A. B. C. D.4.中,是的中点.设则= ,= .ABCDEFABBACDO5.已知中,则下列等式成立的是 .(1) (2)(3) (4)6.已知四边形的对角线与交于点,且求证:四边形是平行四边形.第三课时 向量的减法 (学案)1.若,则= (用表示)2.下列说法中正确的是___________________① 若,则 ② 若,则所在直线平行或重合 ③ 若同向,则 ④ 若,则所在直线重合3.(1)已知,且则= .(2)已知,且则= ;= .4.设表示“向东走”,表示“向西走”,表示“向东走”,表示“向东走”,分别指出下列向量的意义:(1): ;(2): ;(3): ;(4): ;5 . 现 有 下 列 四 个 结 论 : ( 1 ); ( 2 ); ( 3 );(4).其中正确的为 (填上相应的序号).6.已知向量的模分别为 3,4,则的取值范围为 .7.已知非零向量,画图作出下列向量:(1); (2) 8.化简下列各式:(1) (2)选做题:9.已知,求.10.在边长为 的正方形中,已知,求.11. 是平行四边形的对角线的交点,若,求证:.