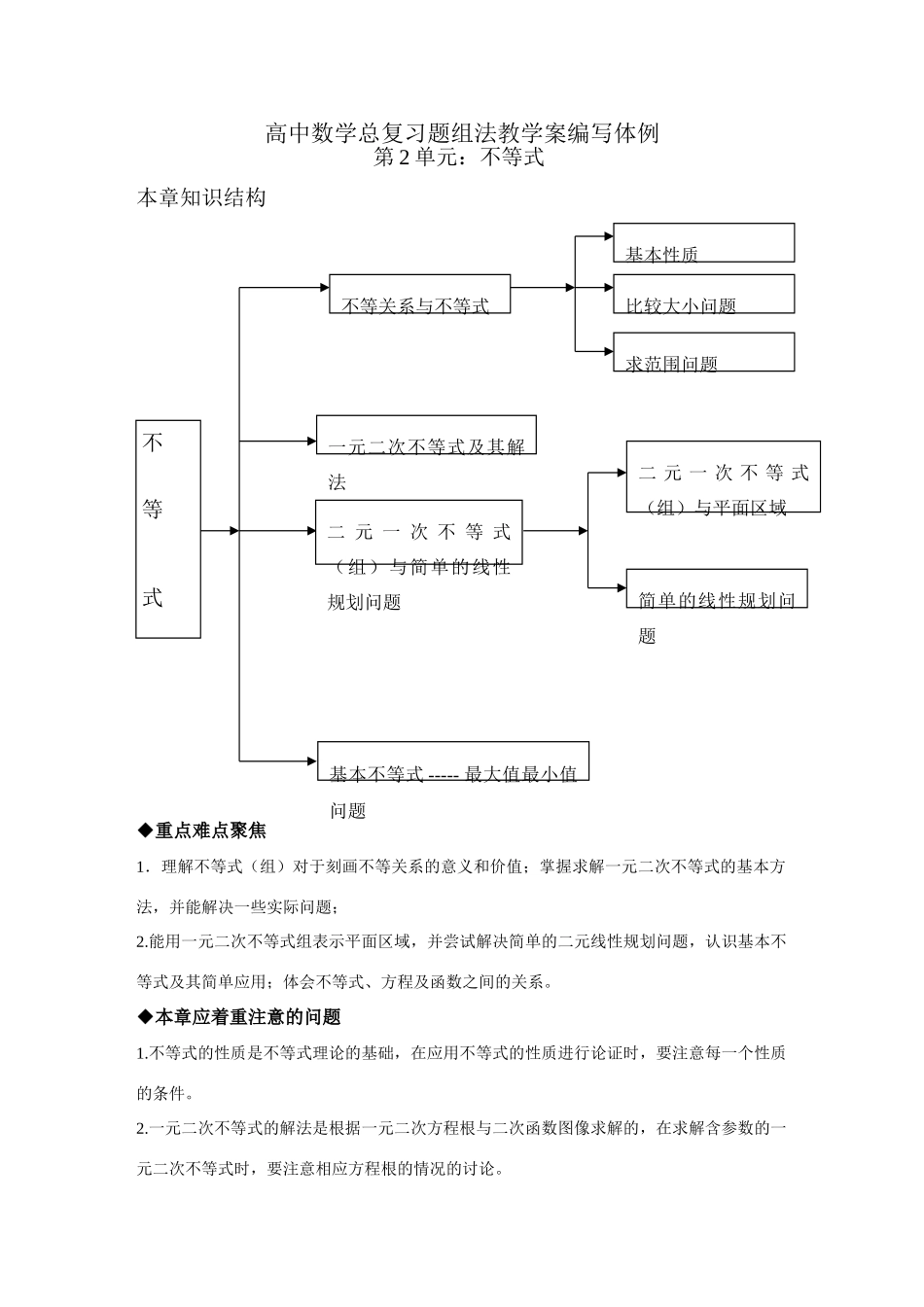
高中数学总复习题组法教学案编写体例第 2 单元:不等式本章知识结构◆重点难点聚焦1.理解不等式(组)对于刻画不等关系的意义和价值;掌握求解一元二次不等式的基本方法,并能解决一些实际问题;2.能用一元二次不等式组表示平面区域,并尝试解决简单的二元线性规划问题,认识基本不等式及其简单应用;体会不等式、方程及函数之间的关系。◆本章应着重注意的问题1.不等式的性质是不等式理论的基础,在应用不等式的性质进行论证时,要注意每一个性质的条件。2.一元二次不等式的解法是根据一元二次方程根与二次函数图像求解的,在求解含参数的一元二次不等式时,要注意相应方程根的情况的讨论。不 等 式不等关系与不等式基本性质比较大小问题求范围问题一元二次不等式及其解法二 元 一 次 不 等 式(组)与简单的线性规划问题简单的线性规划问题基本不等式 ----- 最大值最小值问题二 元 一 次 不 等 式(组)与平面区域3.应用基本不等式求函数最值时,有三个条件:一是 a、b 为正;二是 a+b 与 ab 有一个为正值;三是等号要取到。这三个条件缺一不可,为了达到使用基本不等式的目的,常常需要对函数式(代数式)进行通分、分解等变形,构造和为定值或积为定值的模型。◆高考分析及预测本章内容在高考中属主体内容,以考查不等式性质、解法和最值方面的应用为重点,多数情况是在函数、数列、几何、实际应用题等综合型试题中考查,所占比例为 10%—15%。小题属低中档题、大题属中档以上题,预计在 2009 年高考中,对不等式的性质和解不等式特别是含参数的不等式的解法,仍会继续渗透在其知识中进行考查。对不等式的应用,突出渗透数学思想方法和不等式知识的综合应用,特别是求最值问题、不等式证明问题,将继续强调考查逻辑思维推理能力,尤其是不等式与函数、数列、三角、解析几何的综合题型将会继续出现在高考的中、高档题中。§2.1 不等关系与不等式 1.通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景。2.理解不等式的概念并能用作差法比较两个实数的大小。重点:用不等式(组)表示实际问题中的不等关系,并用不等式(组)研究含有不等关系的问题。理解不等式(组)对于刻画不等式的意义和价值。难点:用不等式(组)正确表示出不等关系。1.不等式的 8 个性质仍是今后高考的热点,它主要用于比较两个实数或式子的大小,以及用于证明一些不等式。它常常与函数、三角、...