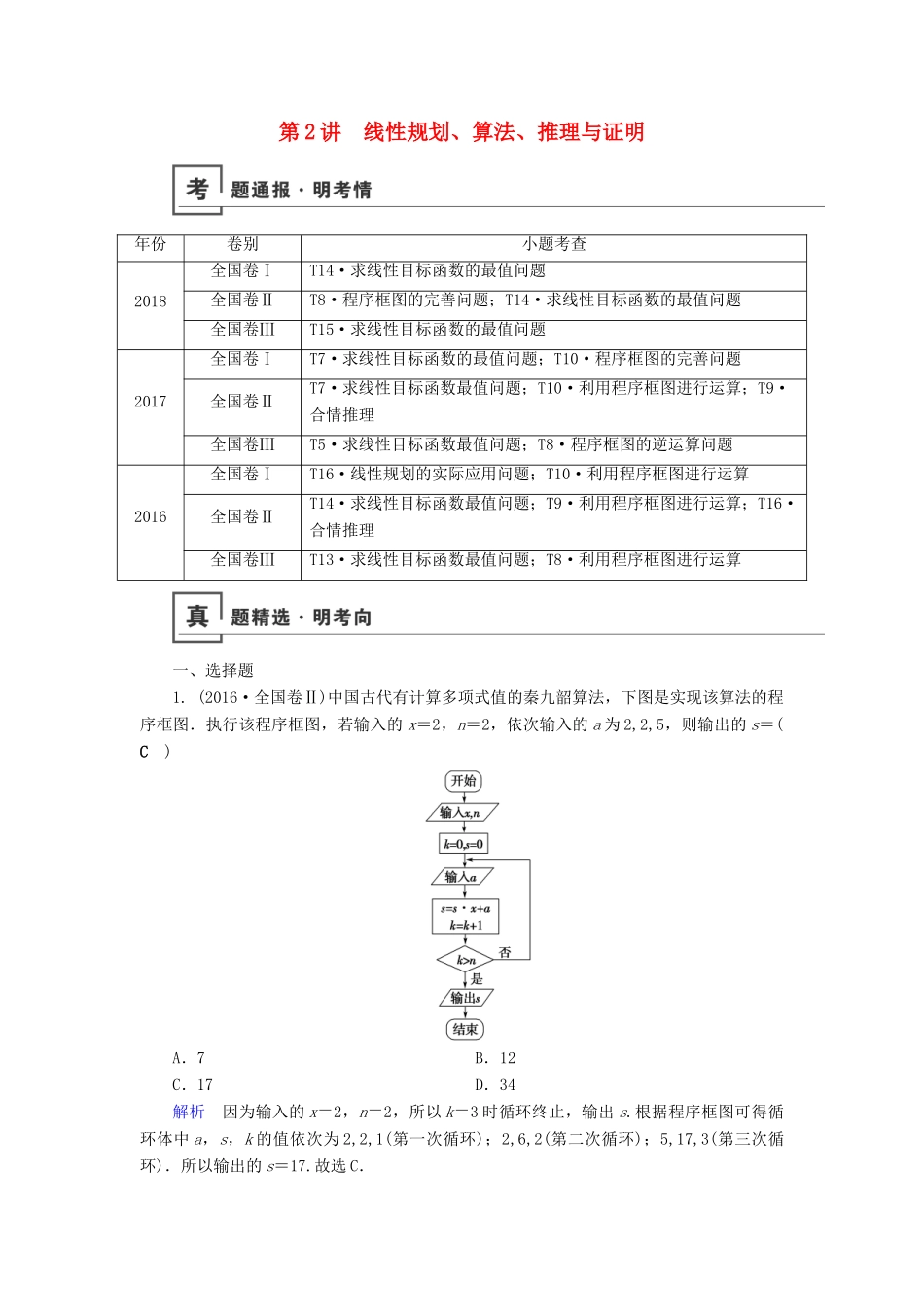
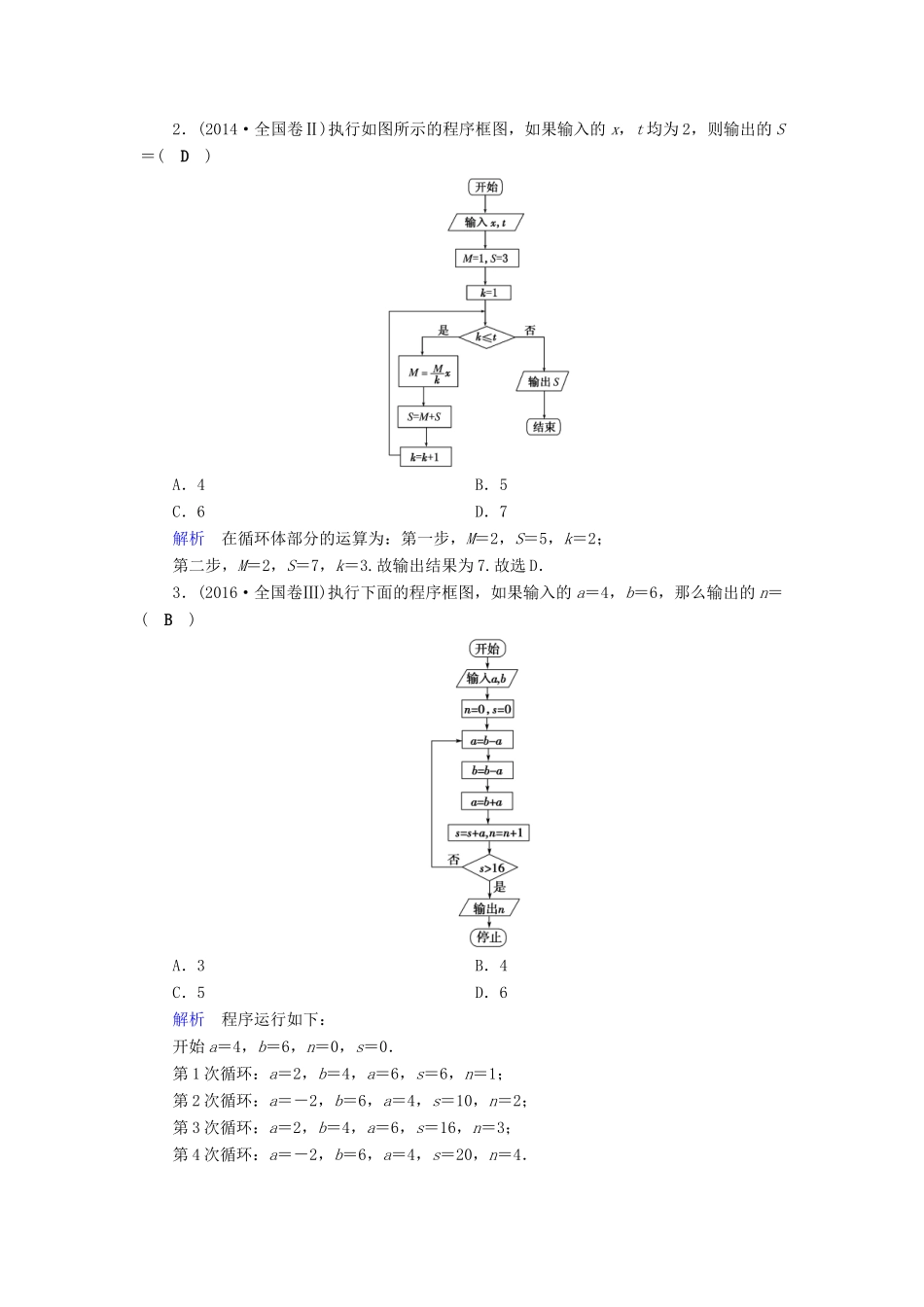
第 2 讲 线性规划、算法、推理与证明年份卷别小题考查2018全国卷ⅠT14·求线性目标函数的最值问题全国卷ⅡT8·程序框图的完善问题;T14·求线性目标函数的最值问题全国卷ⅢT15·求线性目标函数的最值问题2017全国卷ⅠT7·求线性目标函数的最值问题;T10·程序框图的完善问题全国卷ⅡT7·求线性目标函数最值问题;T10·利用程序框图进行运算;T9·合情推理全国卷ⅢT5·求线性目标函数最值问题;T8·程序框图的逆运算问题2016全国卷ⅠT16·线性规划的实际应用问题;T10·利用程序框图进行运算全国卷ⅡT14·求线性目标函数最值问题;T9·利用程序框图进行运算;T16·合情推理全国卷ⅢT13·求线性目标函数最值问题;T8·利用程序框图进行运算一、选择题1. (2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的 x=2,n=2,依次输入的 a 为 2,2,5,则输出的 s=( C )A.7 B.12C.17 D.34解析 因为输入的 x=2,n=2,所以 k=3 时循环终止,输出 s.根据程序框图可得循环体中 a,s,k 的值依次为 2,2,1(第一次循环);2,6,2(第二次循环);5,17,3(第三次循环).所以输出的 s=17.故选 C.2.(2014·全国卷Ⅱ)执行如图所示的程序框图,如果输入的 x,t 均为 2,则输出的 S=( D )A.4 B.5 C.6 D.7解析 在循环体部分的运算为:第一步,M=2,S=5,k=2;第二步,M=2,S=7,k=3.故输出结果为 7.故选 D.3.(2016·全国卷Ⅲ)执行下面的程序框图,如果输入的 a=4,b=6,那么输出的 n=( B )A.3 B.4 C.5 D.6解析 程序运行如下:开始 a=4,b=6,n=0,s=0.第 1 次循环:a=2,b=4,a=6,s=6,n=1;第 2 次循环:a=-2,b=6,a=4,s=10,n=2;第 3 次循环:a=2,b=4,a=6,s=16,n=3;第 4 次循环:a=-2,b=6,a=4,s=20,n=4.此时,满足条件 s>16,退出循环,输出 n=4.故选 B.4.(2015·全国卷Ⅰ)执行如图所示的程序框图,如果输入的 t=0.01,则输出的 n=( C )A.5 B.6 C.7 D.8解析 运行第一次:S=1-==0.5,m=0.25,n=1,S>0.01;运行第二次:S=0.5-0.25=0.25,m=0.125,n=2,S>0.01;运行第三次:S=0.25-0.125=0.125,m=0.062 5,n=3,S>0.01;运行第四次:S=0.125-0.062 5=0.062 5,m=0.031 25,n=4,S>0.01;运行第五次:S=0.031 25,m=0.015 625,n=5...