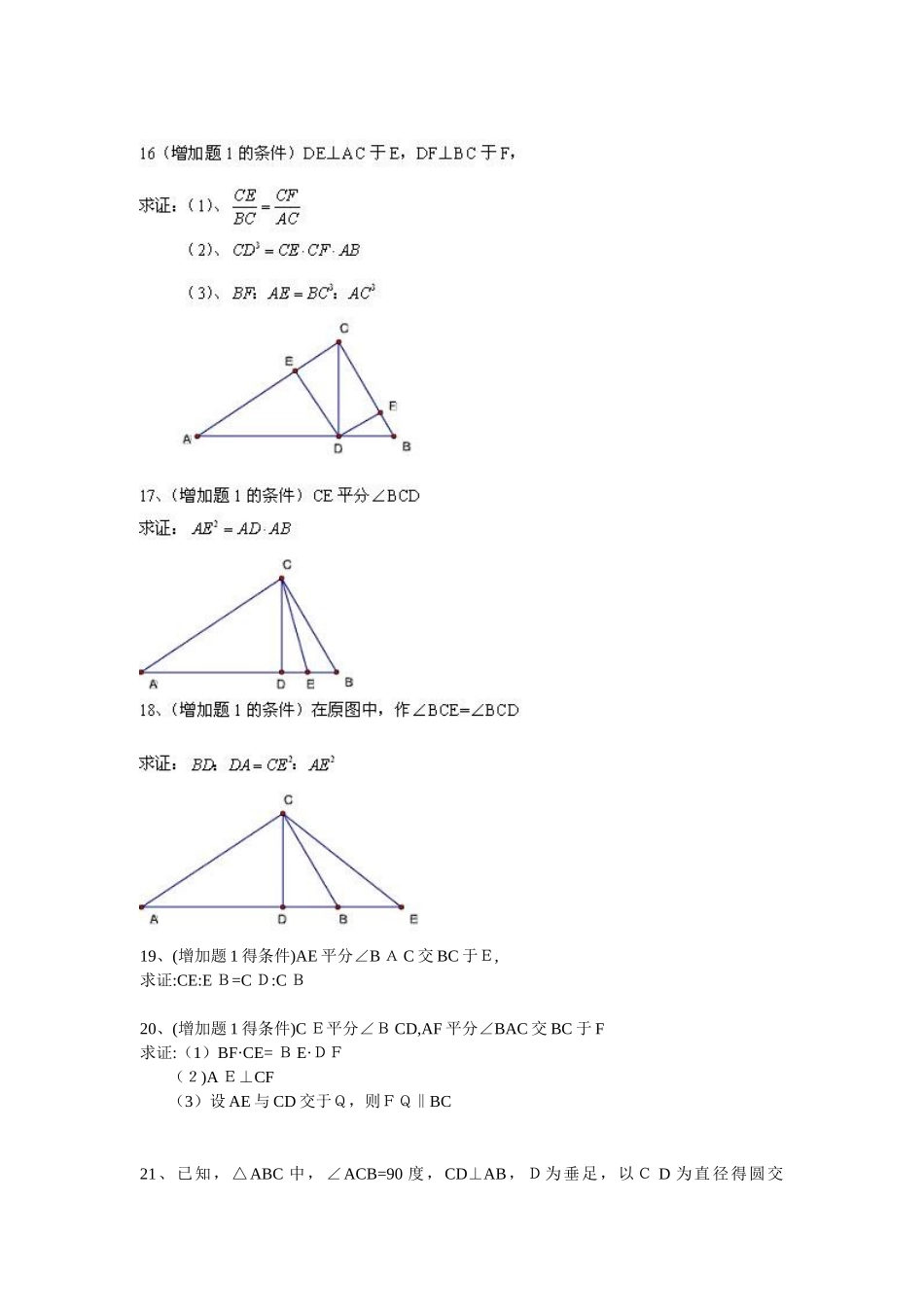
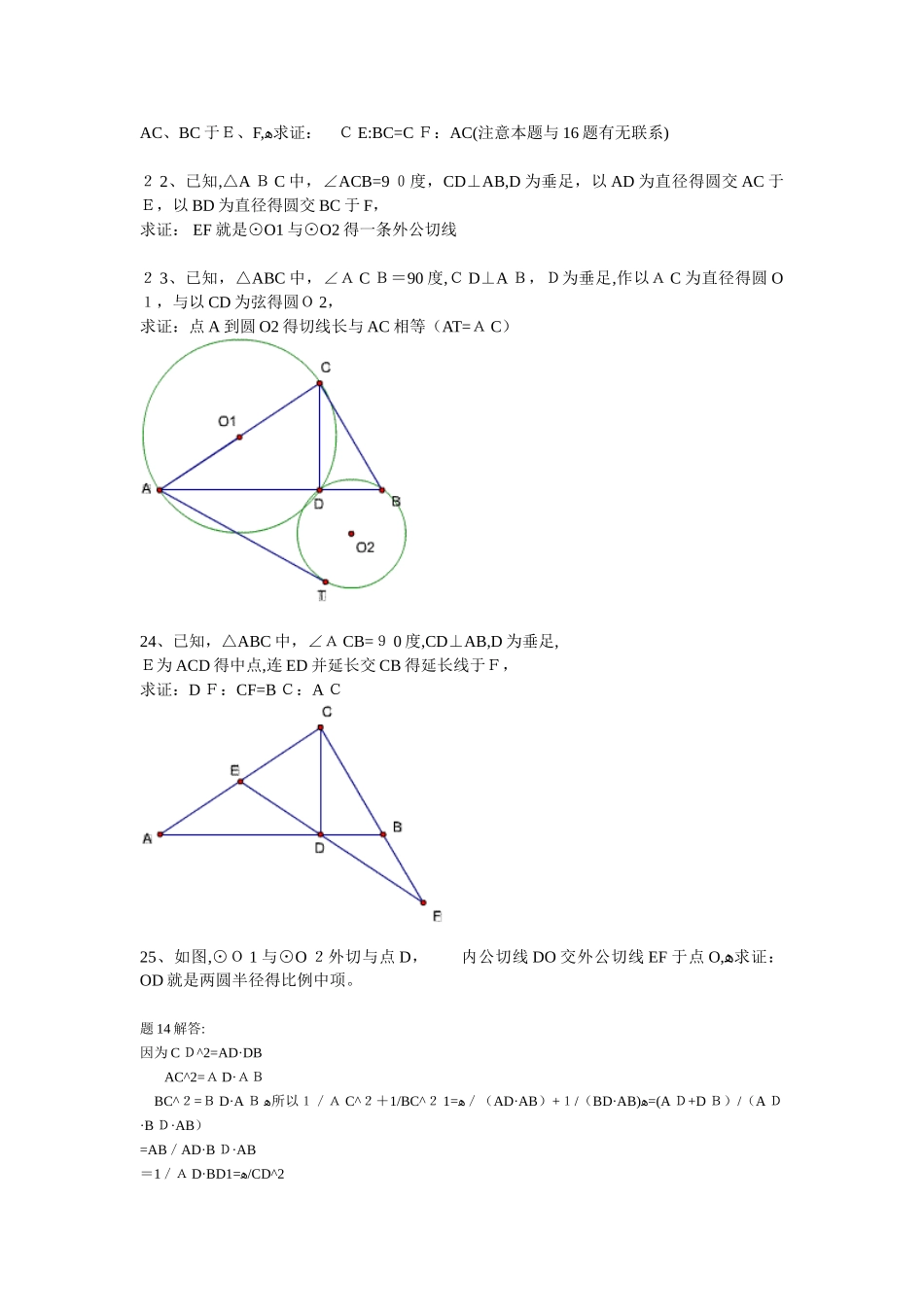
平面几何一题多变ﻫ在完成一个数学题得解答时,有必要对该题得内容、形式、条件、结论 ,做进一步得探讨,以真正掌握该题所反映得问题得实质。假如能对一个普通得数学题进行一题多变,从变中总结解题方法;从变中发现解题规律,从变中发现“不变",必将使人受益匪浅。ﻫ“一题多变”得常用方法有:1、变换命题得条件与结论;2、保留条件,深化结论;3、减弱条件,加强结论;ﻫ4、探讨命题得推广;ﻫ5、考查命题得特例;ﻫ6、生根伸枝,图形变换;7、接力赛,一变再变;ﻫ8、解法得多变等。ﻫ19、(增加题 1 得条件)AE 平分∠B A C 交 BC 于E,求证:CE:E B=C D:C B20、(增加题 1 得条件)C E平分∠B CD,AF 平分∠BAC 交 BC 于 F求证:(1)BF·CE= B E·DF (2)A E⊥CF (3)设 AE 与 CD 交于Q,则FQ‖BC21、已知,△ABC 中,∠ACB=90 度,CD⊥AB,D为垂足,以C D 为直径得圆交AC、BC 于E、F,ﻫ求证: C E:BC=C F:AC(注意本题与 16 题有无联系)2 2、已知,△A B C 中,∠ACB=9 0度,CD⊥AB,D 为垂足,以 AD 为直径得圆交 AC 于E,以 BD 为直径得圆交 BC 于 F,求证: EF 就是⊙O1 与⊙O2 得一条外公切线2 3、已知,△ABC 中,∠A C B=90 度,C D⊥A B,D为垂足,作以A C 为直径得圆 O1,与以 CD 为弦得圆O 2,求证:点 A 到圆 O2 得切线长与 AC 相等(AT=A C)24、已知,△ABC 中,∠A CB=9 0 度,CD⊥AB,D 为垂足,E为 ACD 得中点,连 ED 并延长交 CB 得延长线于F,求证:D F:CF=B C:A C25、如图,⊙O 1 与⊙O 2外切与点 D, 内公切线 DO 交外公切线 EF 于点 O,ﻫ求证:OD 就是两圆半径得比例中项。题 14 解答:因为 C D^2=AD·DB AC^2=A D·AB BC^2=B D·A Bﻫ所以1/A C^2+1/BC^2 =ﻫ1/(AD·AB)+1/(BD·AB)ﻫ=(A D+D B)/(A D·B D·AB)=AB/AD·B D·AB=1/A D·BD =ﻫ1/CD^215 题解答:因为 M 为 AB 得中点,所以 AM=MB,A D-DB=AM+DM-(MB-DM)=2 D MAC^2—BC^2=AD*A B-DB*ABﻫ =(A D—DB)A B =2 D M*AB2 6、(在 1 9题基础上增加一条平行线)已知,△ABC 中,∠ACB=9 0度,C D⊥AB,D 为垂足,A E 平分∠BA C交 BC 于 E、交C D 于 F,FG‖AB 交B C 于点 G,ﻫ求证:CE=B G2 7...