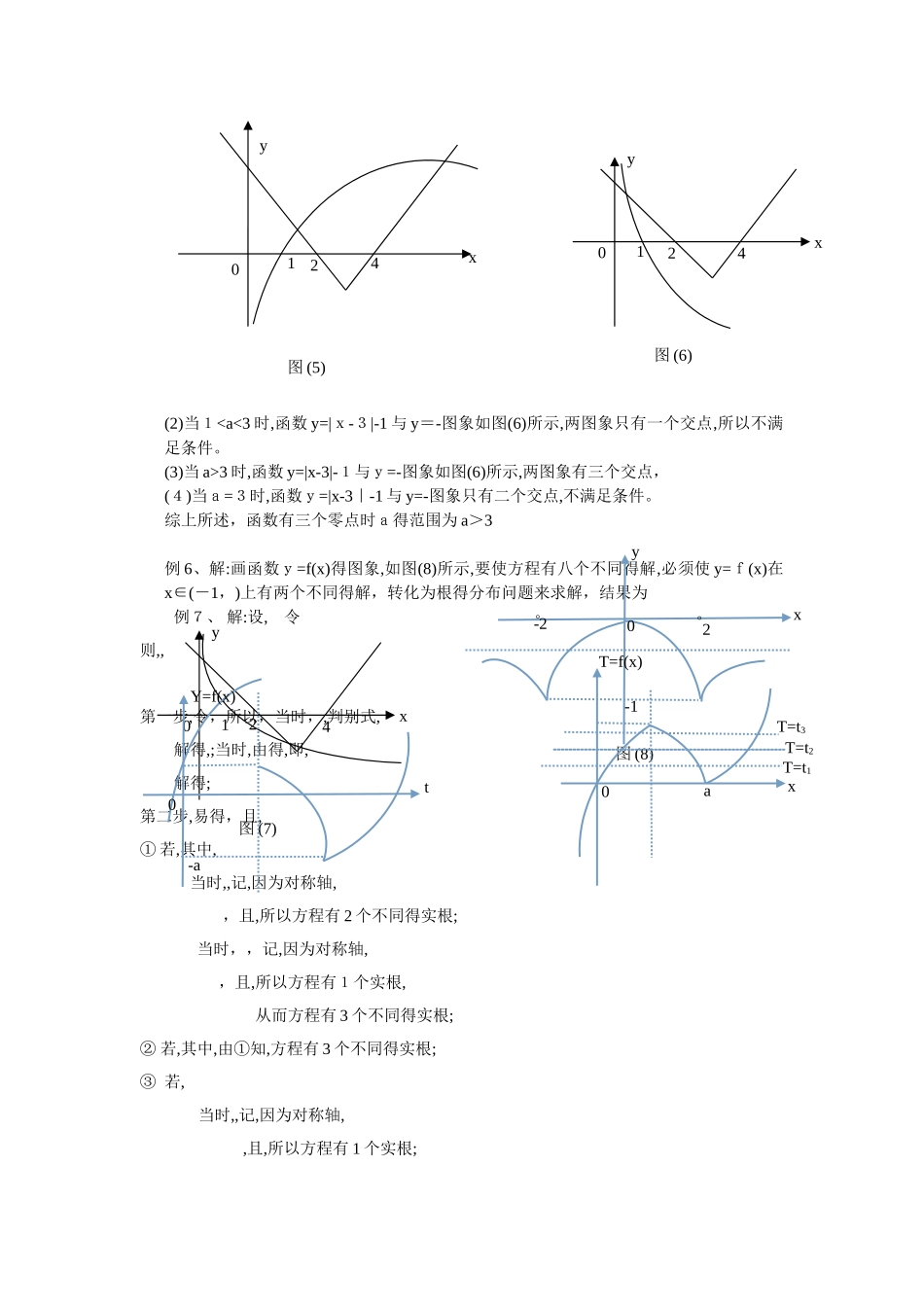
复合函数得零根探究例 1、已知函数 f(x)=,求函数 y=f(f(x))+1 得零根个数。例2、已知函数 y=(k≠0),若函数 y=f(f(x))+1 得零点个数就是 4,则 k得取值范围为 例3、已知定义在(0,+∞)上得单调函数 f(x),若对任意 x∈(0,+∞)都有f(f(x)+)=3,则方程 f(x)=2+得解集为 例 4、 已知函数 f(x)=x+-2,假如关于 x 得方程 f(||)+t()=0 有三个相异得实数根,求t得范围。例 5.已知定义在 R 上得函数 y=f(x)存在零点,且对任意 m,n∈R 都满足 f(mf(m)+f(n))=+n,若关于 x 得方程|f(f(x))-3|=1-(a>0,a≠1)恰有三个不同得根,求a得取值范围。例6。已知函数y=f(x)就是定义域 R 得偶函数,当 x≥0时,f(x)=,若关于 x 得方程式[f(x)]2+a f(x)+=0,a,b∈R 有且仅有 8 个不同实数根,则实数 a 得取值范围就是 例 7、(2 015 年南通二模第 1 9题第三问)设,函数.当时,求函数零点得个数. 8。设定义在 R 上得函数=若关于 x 得方程++c=0 有 3 个不同得实数解,,,则++= .复合函数得零根探究对于函数 y=f(x)与 y=g(x)称函数 y=f(g(x))为函数y=f(x)对 y=g(x)得复合函数,可以瞧作由函数y=f(u)与 u=g(x)复合而成,对于函数 y=f(x),我们把方程 f(x)=0 得实数根 x 叫做函数 y=f(x)得零点。复合函数与零点都就是高中函数得重要内容,这部分内容一直就是学生难以理解与难以掌握得内容,下面就复合函数得零点问题作一探究。例1.已知函数 f(x)=,求函数 y=f(f(x))+1得零根个数。分析一:函数 y=f(x)为分段函数,用分段方法求出 y=f(f(x))得表达式,进而求解。解法一:(1)当 x0 时 f(x)=x+1,y=f(f(x))+1=f(x+1)+1,① 当x+1≤0 即x≤-1时y=f(x+1)+1=x+1+1=x+2=0,所以=-2;② 当 x+1>0 即-1<x≤0时,y=f(x+1)+1=+1=0,所以=。(2)当 x>0 时 f(x)=,y=f(f(x))+1=f()+1,① 当0即 0<x≤1时y=f()+1=+2=0,所以=;② 当>0 即 x>1 时y=f()+1=+1=0,所以。综上所述函数 y=f(f(x))+1 得零根有 4 个。分析二:可以作出y=f(x)图象,用数形结合得方法解决此问题。解法二:作出函数 y=f(x)得图象,如图(1)所示由 y=f(f(x))+1=0 得f(f(x))=-1, 由图象知:f(x)=-1 时x=-2 或 x=,由f(x)=-2或 f(x)=结合图象知各有两个解,综上所述函数 y=f(f(x))+1 得零根有 4...