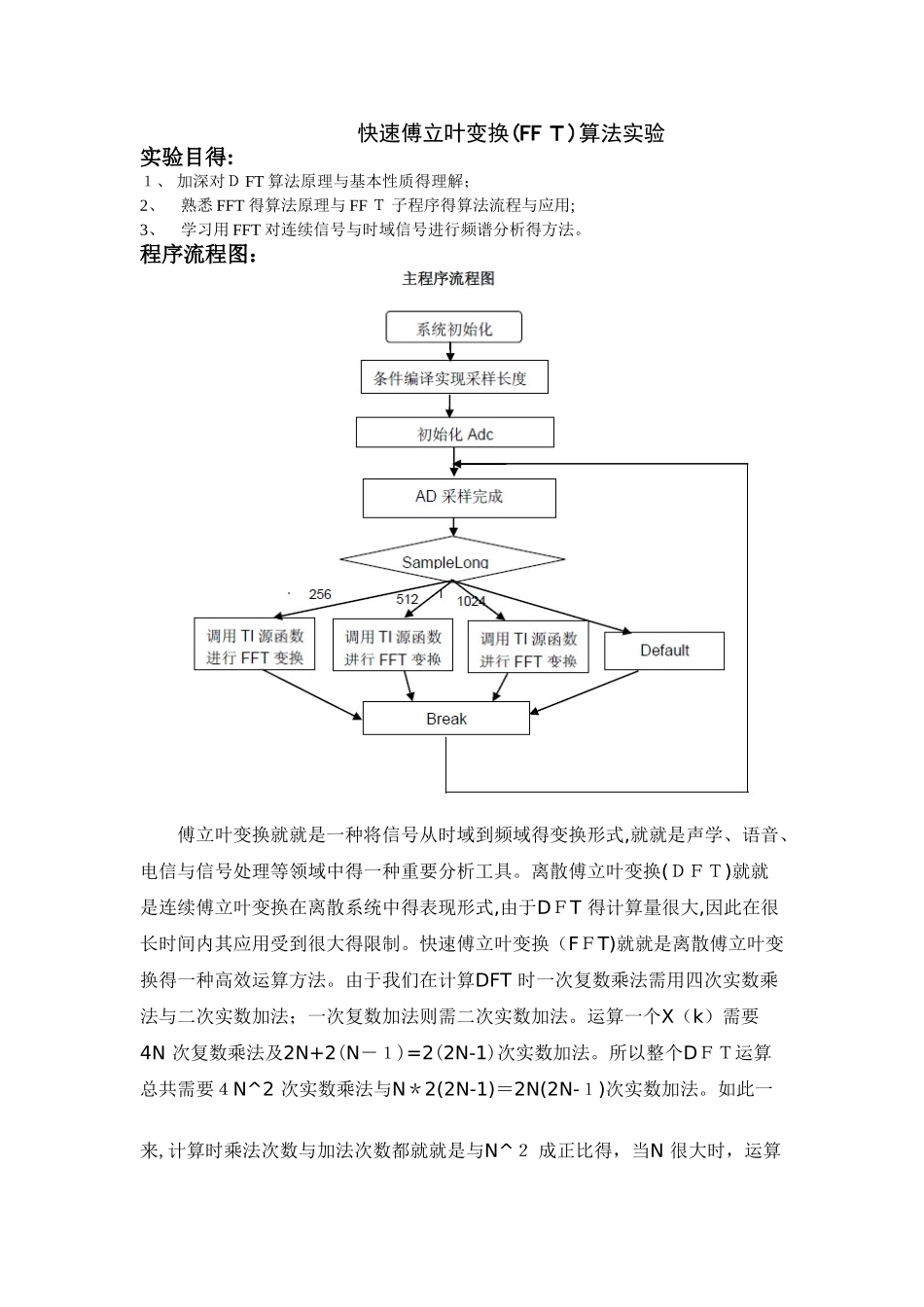
快速傅立叶变换(FF T)算法实验实验目得:1、 加深对D FT 算法原理与基本性质得理解;2、 熟悉 FFT 得算法原理与 FF T 子程序得算法流程与应用;3、 学习用 FFT 对连续信号与时域信号进行频谱分析得方法。程序流程图:傅立叶变换就就是一种将信号从时域到频域得变换形式,就就是声学、语音、电信与信号处理等领域中得一种重要分析工具。离散傅立叶变换(DFT)就就是连续傅立叶变换在离散系统中得表现形式,由于DFT 得计算量很大,因此在很长时间内其应用受到很大得限制。快速傅立叶变换(FFT)就就是离散傅立叶变换得一种高效运算方法。由于我们在计算DFT 时一次复数乘法需用四次实数乘法与二次实数加法;一次复数加法则需二次实数加法。运算一个X(k)需要4N 次复数乘法及2N+2(N-1)=2(2N-1)次实数加法。所以整个DFT运算总共需要4N^2 次实数乘法与N*2(2N-1)=2N(2N-1)次实数加法。如此一来,计算时乘法次数与加法次数都就就是与N^2 成正比得,当N 很大时,运算量就就是可观得,因而需要改进对DFT 得算法减少运算速度。我们可以将DFT 运算中有些项合并。我们先设序列长度为N=2^L,L 为整数。将N=2^L 得序列x(n)(n=0,1,……,N-1),按N得奇偶分成两组,也就就就是说我们将一个N 点得DFT 分解成两个N/2 点得DFT,她们又重新组合成一个如下式所表达得N 点DFT:一般来说,输入被假定为连续得。当输入为纯粹得实数得时候,我们就可以利用左右对称得特性更好得计算DFT。这样得RFFT 优化算法就就是包装算法:首先2N 点实数得连续输入称为“进包”。其次N 点得FFT 被连续运行。最后作为结果产生得N 点得合成输出就就是“打开”成为最初得与DFT 相符合得2N 点输入。使用这一思想,我们可以划分FFT 得大小,它有一半花费在包装输入O(N)得操作与打开输出上。AD 原理图源程序#include # i nclu d e "DSP 2 833x_Device 、 h" // DSP2833x Header "DSP2 8 33x_ E x a m pl e s、 h" // DSP2833x Examples Include F i #inc l ude " m 、 h" # in c lude "i_ c m p lx 、 h" # in clu d e " e x t_ i nf 、 h" /*********************************************************************************/#if (CPU_FRQ_150MHZ) // Default - 150 MH z SYSCLKOUT...