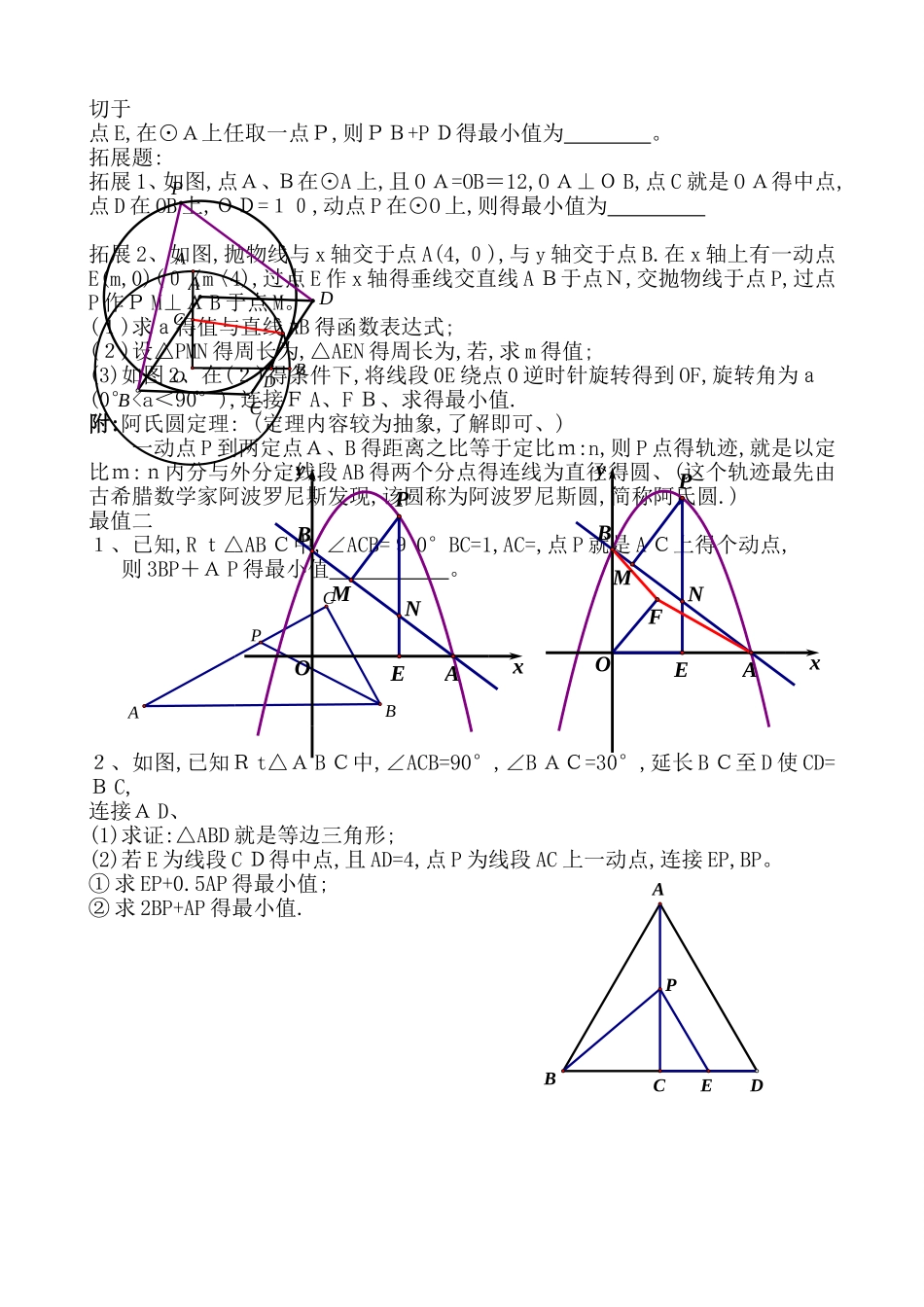
201 9届初中数学总复习微专题构造母子型相似解决阿氏圆题型何求 2025。6.10阿氏圆题型就是这几年在中考中也就是逐渐火热,出题频率越来越高,成为近几年中考填空、解答得压轴热点题型。阿氏圆题型,很多同学感觉困难,但就是掌握了特点与方法,困难就能迎刃而解!一、阿氏圆题型:例、在Rt△AB C中,∠AOB=9 0°,AO=3,B O=4,⊙O 得半径为 2,P 为⊙O上一动点,则得最小值为 、 二、阿氏圆题型特点:动点 P 在圆 (圆弧)上运动且圆心 O 到动点 P 得距离 O P与圆心O到定点 B 得距离 OB 得比值为定值 k,求 PA+k·P B (k≠1)最小值得题型、三、阿氏圆解题方法:初中数学解决阿氏圆问题,要熟练掌握母子型相似三角形得性质与构造方法、构造母子型三角形相似,结合两点之间线段最短进行求解就就是解决阿氏圆题型得核心武器!步骤如下:(口诀:找母作子定最值)1.找母三角形:标出半径(圆心到动点得线段OP)与定线段(圆心到定点得线段OB)及其夹角(∠BO P)得三角形;2.作子三角形:利用标出两边得夹角,构造一条线段,使其长度与半径比为 K,构造出子三角形,由于共角,那么母子三角形相似;3、 得到去除系数k得线段,结合两点之间线段最短进行求解。 例 1、在 Rt△A OB中,∠A O B=9 0°,A O=3,B O=4,⊙O 得半径为2,P 为⊙O 上一动点,则得最小值为 . 基本思路:构造母子型三角形相似,将(1/2)PB 转化成(P E/PB)=(1/2), 只需求 PA+PE 最小,结合两点之间线段最短进行求解。解:在 O B上截取 OE=(1/2)O P,连接 PE。 (O P/OB)=(O E/O P)=(1/2),∠PO B=∠EOP ∴△POB∽△EOP ∴P E=(1/2)P B=1 ∴P A+(1/2)P B=P A+PE 当点 E、P、A 三点共线时,PA+PE 最小, 即 PA+(1/2)P B得最小值为√((1^2)+(3^2))=√(10) 练习1、已知正方形 ABCD 得边长为 4,圆B得半径为 2 点 P 就是圆 B 上得个动点,求 PD+½P C得最小值 .练习 2、在正方形 A BC D 中,G 为正方形内一点,AD=4,P 为 BC 中点,且BG=BP,则得最小值就是 。例2、在平面直角坐标系中,A(2,0),B(0,2),C(4,0),D(3,2),P就是△AOB 外部得第一象限内一动点,且∠BPA=135°,则 2PD+PC 得最小值就是 、练习 3、如图,已知菱形 AB C D 得边长为 4,∠B=6 0°,点E、F 分别就是A B、BC得中点,点P在菱形内部,且∠EP F=1 50°,则得最小值为 、练习4、练...