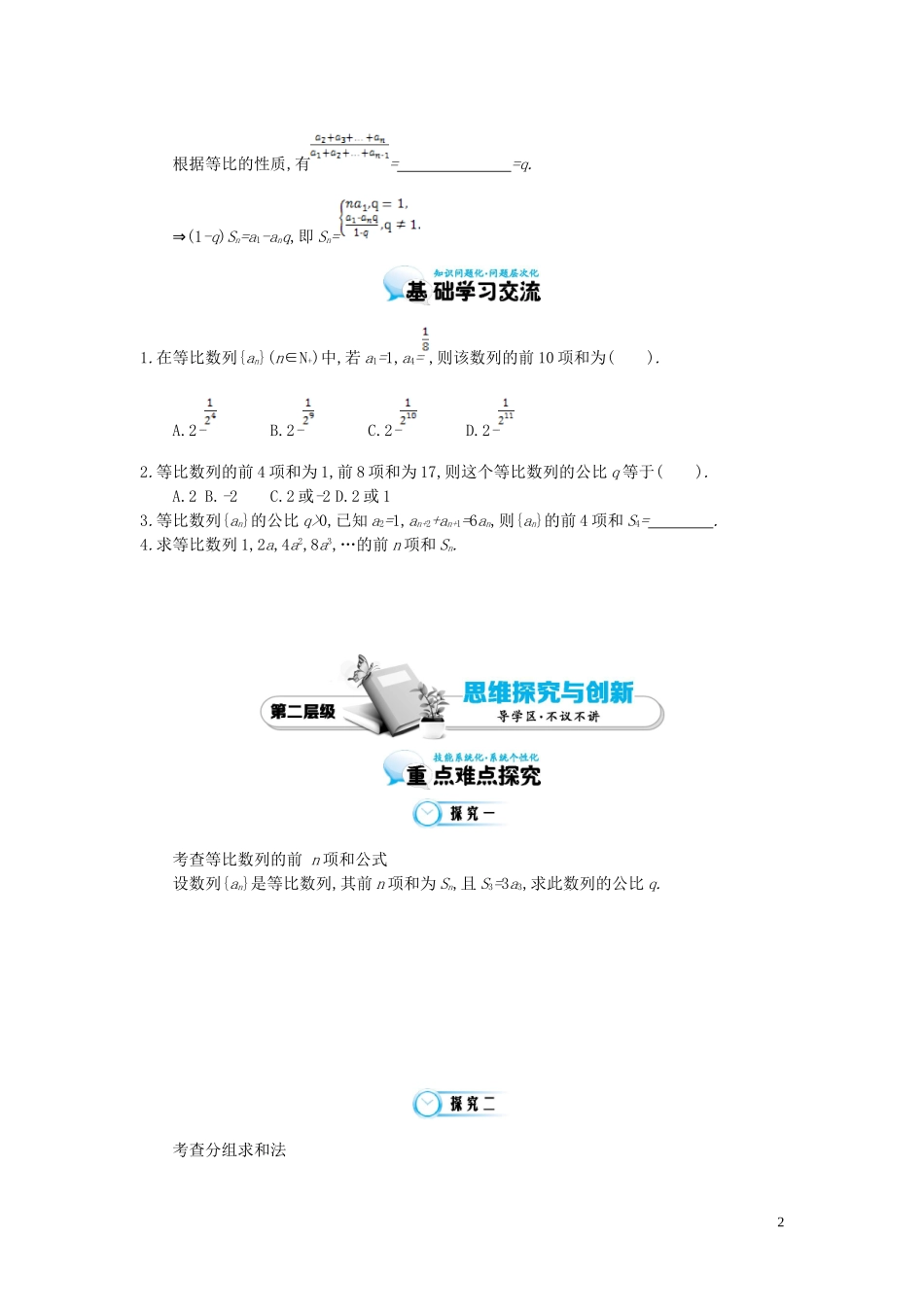
第 7 课时 等比数列的前 n 项和1.掌握等比数列的前 n 项和公式的推导方法.2.应用等比数列的前 n 项和公式解决有关等比数列的问题.3.会求等比数列的部分项之和.印度的舍罕王打算奖赏发明国际象棋的大臣西萨·班·达依尔,并问他想得到什么样的奖赏.大臣说:“陛下,请您在这张棋盘的第一个小格内赏给我一粒麦子,在第二个小格内给两粒,在第三个小格内给四粒,照这样下去,每一小格内都比前一小格内的麦子数增加一倍,直到把每一小格都摆上麦子为止,并把这样摆满棋盘上六十四格的麦子赏给您的仆人.”国王认为这位大臣的要求不算多,就爽快地答应了.国王能实现他的诺言吗? 问题 1:等比数列的前 n 项和公式:当 q=1 时,Sn= ; 当 q≠1 时,Sn= = . 问题 2:我们来帮国王计算下要多少粒麦子,把各格所放的麦子数看成是一个数列{an},它是一个 a1=1,q=2,n=64 的等比数列,问题转化为求数列{an}的前 64 项的和,可求得 Sn= = =264-1,而 264-1 这个数很大,超过了 1.84×1019,所以国王根本实现不了这个诺言. 问题 3:用错位相减法来推导等比数列的前 n 项和公式:设等比数列{an}的公比为 q,它的前 n 项和是 Sn=a1+a1q+a1q2+…+a1qn-1. ①①×q 得 qSn=a1q+a1q2+…+a1qn-1+a1qn. ②①-② 得(1-q)Sn= . 当 q=1 时,该数列是常数列,Sn= ; 当 q≠1 时,该等比数列的前 n 项和公式为:Sn= . 即 Sn=问题 4:用等比数列的定义推导等比数列的前 n 项和公式:由等比数列的定义,有 = =…==q.1根据等比的性质,有= =q. (1⇒-q)Sn=a1-anq,即 Sn=1.在等比数列{an}(n∈N+)中,若 a1=1,a4= ,则该数列的前 10 项和为( ).A.2- B.2- C.2- D.2-2.等比数列的前 4 项和为 1,前 8 项和为 17,则这个等比数列的公比 q 等于( ).A.2 B.-2C.2 或-2 D.2 或 13.等比数列{an}的公比 q>0,已知 a2=1,an+2+an+1=6an,则{an}的前 4 项和 S4= . 4.求等比数列 1,2a,4a2,8a3,…的前 n 项和 Sn.考查等比数列的前 n 项和公式设数列{an}是等比数列,其前 n 项和为 Sn,且 S3=3a3,求此数列的公比 q.考查分组求和法2已知{an}是各项均为正数的等比数列,且 a1+a2=2( + )=8( + ).(1)求{an}的通项公式;(2)设 bn=+log2an,求数列{bn}的前 n 项和 Tn.对变量的分类讨论Sn是无穷等比数列{an}的前 n 项和,且公比 q≠1,已知 1 是 S2和 S3的等差中项,6 是 2S2和 3S3的等比中项.(1)求 S2和 S3;(2)求此数列{an}...