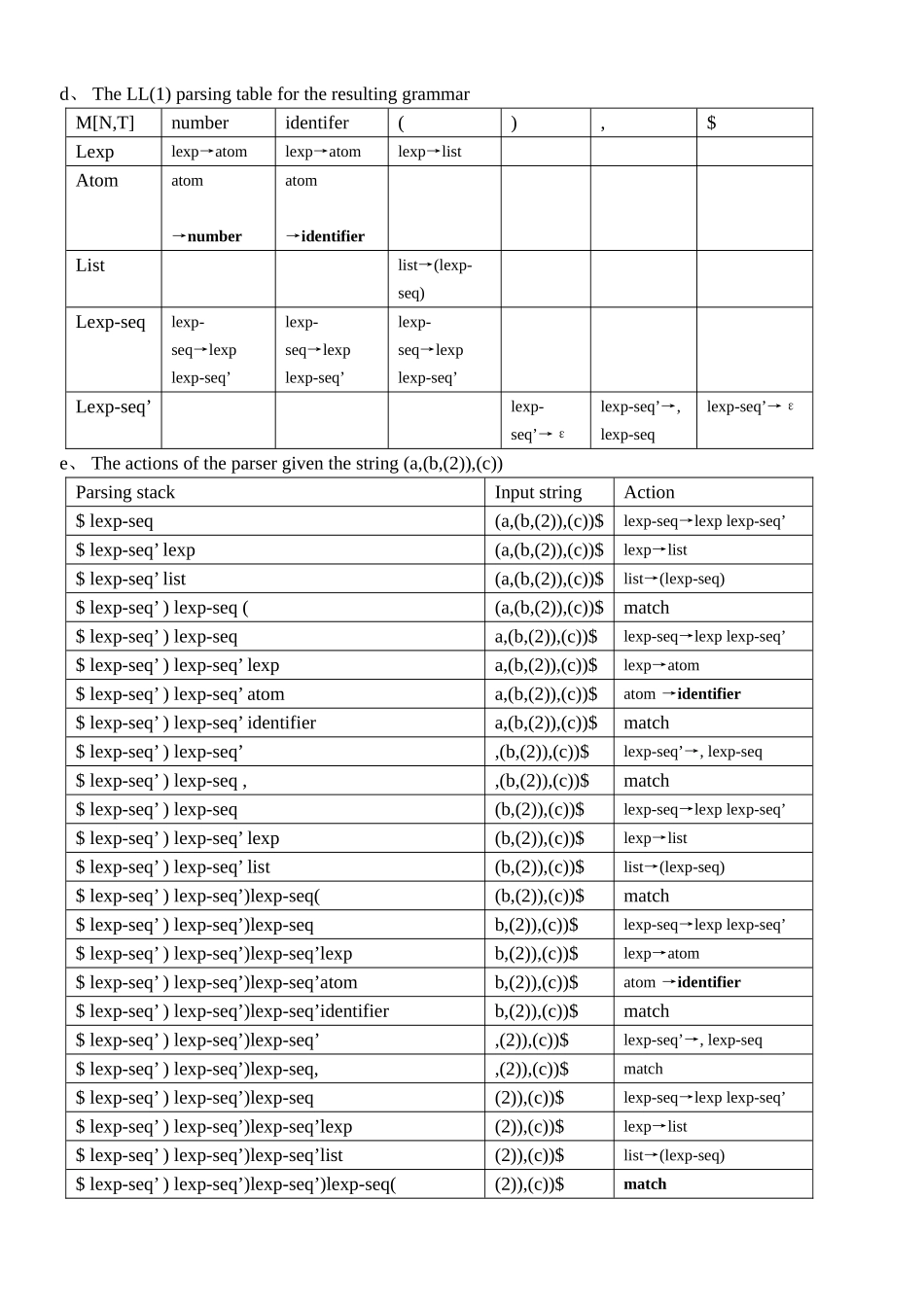
The exercises of Chapter Four4、2 Grammar: A → ( A ) A | ε Assume we have lookahead of one token as in the example on p、 144 in the text book、 Procedure A() if (LookAhead() ∈ {‘(‘}) then Call Expect(‘(‘) Call A() Call Expect (‘)’) Call A() else if (LookAhead() ∈ {‘)‘, $}) then return() else /* error */ fi fi end 4、3 Given the grammar statement→ assign-stmt|call-stmt|otherassign-stmt→identifier:=expcall-stmt→identifier(exp-list)[Solution]First, convert the grammar into following forms:statement→ identifier:=exp | identifier(exp-list)|otherThen, the pseudocode to parse this grammar:Procedure statementBeginCase token of( identifer : match(identifer);case token of( := : match(:=); exp;( (: match((); exp-list;match());else error;endcase(other: match(other);else error;endcase;end statement4、7 a Grammar: A → ( A ) A | ε First(A)={(,ε } Follow(A)={$,)}4、7 bSee theorem on P、178 in the text book1.First{(}∩First{ε}=Φ2.ε∈Fist(A), First(A) ∩Follow(A)= Φboth conditions of the theorem are satisfied, hence grammar is LL(1)4、9 Consider the following grammar:lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp, lexp-seq|lexpa、 Left factor this grammar、b、 Construct First and Follow sets for the nonterminals of the resulting grammar、c、 Show that the resulting grammar is LL(1)、d、 Construct the LL(1) parsing table for the resulting grammar、e、 Show the actions of the corresponding LL(1) parser, given the input string (a,(b,(2)),(c))、[Solution]a、lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp lexp-seq’lexp-seq’→, lexp-seq|εb、First(lexp)={number, identifier, ( }First(atom)={number, identifier}First(list)={( }First(lexp-seq)={ number, identifier, ( }First(lexp-seq’)={, , ε}Follow(lexp)={, $, } }Follow(at...