不定积分第一类换元法

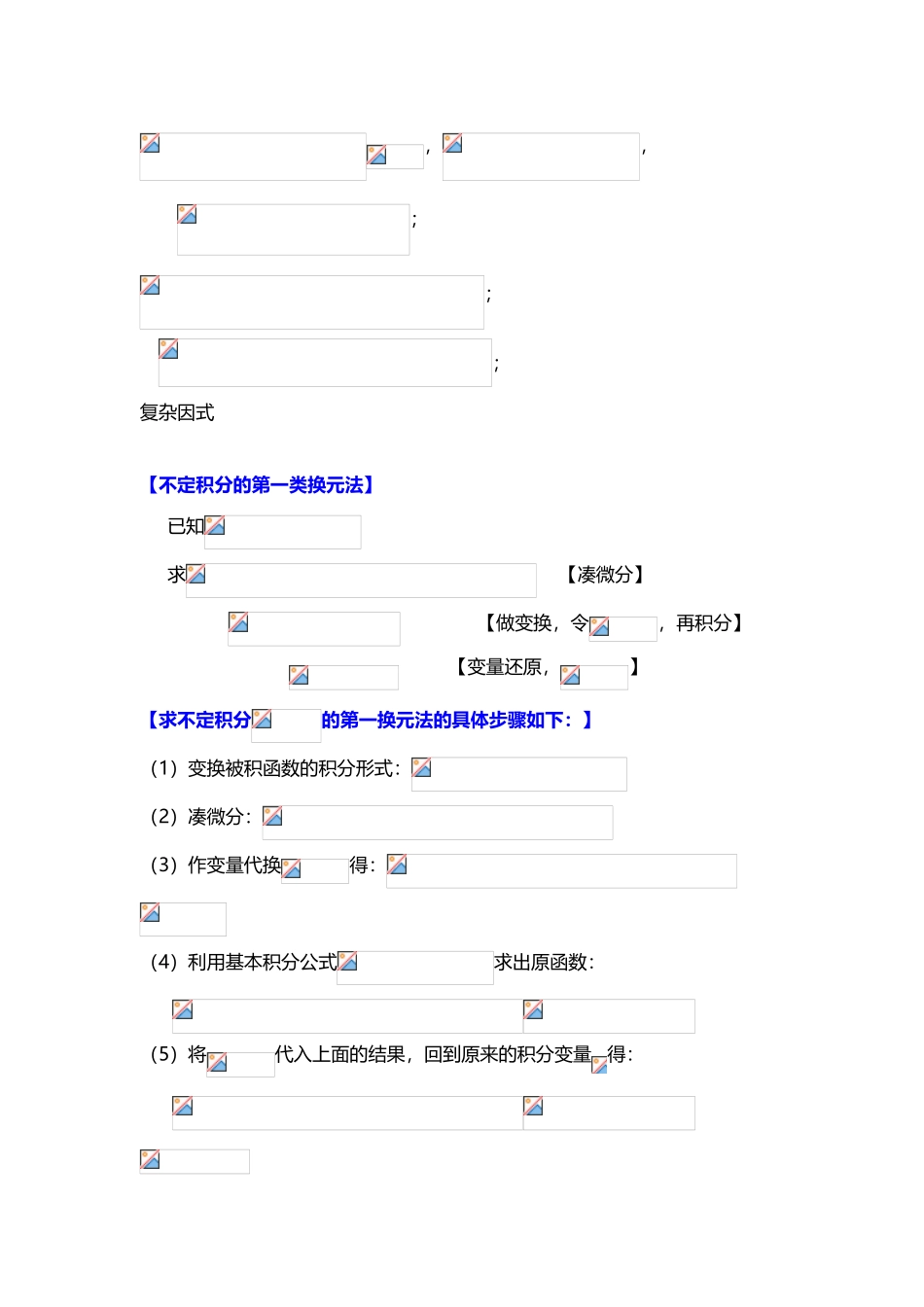
不定积分第一类换元法(16页)Good is good, but better carries it.精益求精，善益求善。不定积分第一类换元法（凑微分法）一、 方法简介设具有原函数，即，，假如是中间变量，，且设可微，那么根据复合函数微分法，有从而根据不定积分的定义得.则有定理：设具有原函数，可导，则有换元公式由此定理可见，虽然是一个整体的记号，但如用导数记号中的及可看作微分，被积表达式中的也可当做变量的微分来对待，从而微分等式可以方便地应用到被积表达式中。几大类常见的凑微分形式： ；，，，；，；，，；；；复杂因式【不定积分的第一类换元法】 已知 求 【凑微分】 【做变换，令，再积分】 【变量还原，】【求不定积分的第一换元法的具体步骤如下：】（1）变换被积函数的积分形式：（2）凑微分：（3）作变量代换得：（4）利用基本积分公式求出原函数： （5）将代入上面的结果，回到原来的积分变量得： 【注】熟悉上述步骤后，也可以不引入中间变量，省略(3)(4)步骤，这与复合函数的求导法则类似。二、典型例题 ；例 1. 例 2. [1]例 3. [1] 例 4.[1]1．解：令,,2．解：令， 3．解： 令 原式 4．解： ，，，；例 1.[2] 例 2. [2]例 3.[1] 例 4.[1] 例 5.[1] 例 6.[1]例 7.设为常数，且，计算[1]1.解：设，， 2．解： 3．解： 4.解： 5.解： 6.解：令，再令，有 7．解： ，；例 1.[3] 例 2.[2]例 3.[2] 例 4.[2]例 5.[1] 例 6.[1]例 7.[1] 例 8.[2]1.解： 2.解 ：令， 3.解：令，， 4.解：令， 5.解： 6.解： 7.解： 令,,, 原式 8.解： ，，；例 1.[2] 例 2.[4]例 3.[4] 例 4.[1]例 5[1] 例 6. [1]例 7[1]1.解： 2.解： 3.解： 对于右端第一个积分，凑微分得 第二个积分中，用代换 原式4.解： 5.解： 6.解： 7.解： ；例 1.[3] 例 2. [4]例 3.[1] 例 4.[1]例 5.[1]1.解：2.解： 3.解： 4．解： 5．解： 令， 复杂因式例 1.[4] 例 2.[1]例 3.[1] 例 4.[1]例 5.[1] 例 6.[1]1.解： 2.解：3.解： 4.解： 5.解： 6.解： 1．在下列各式等号右端的空白处填入适当的系数，使等式成立：(1) dx  d(ax+b)(a≠0)； (2) dx d(7x3)；(3) xdx d(5)； (4) xdx d(1)；(5) dx d(32); (6) dx d()；(7) dx d(1+); (8)  d(5ln｜x｜);(9)  d(1arcsinx); (10)  d;(11)  d(arctan3x); (12)...